练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
    如图，将自然数1，2，3，…，按箭头所指方向顺序排列，依次在2，3，5，7等数的位置拐弯，如数2算做第一次拐弯处，那么第15次拐弯处的数是（　　）
    分析：解这类题目最好是能找到拐弯次数n与拐弯处的数之间的关系，观察可以发现，当n 为奇数时为1+（1+3+5+…+n）=(
    n+1
    2
    )    2    +1，据此即能求出那么第15次拐弯处的数是多少．
    解答：解：观察拐弯处的数的规律，可以得到 n个拐弯处的数，
    当n 为奇数时为：1+（1+3+5+…+n）=(
    n+1
    2
    )    2    +1，
    所以第15次拐弯处的数是：(
    15+1
    2
    )    2    +1=65．
    故选：B．
    点评：从拐弯处数字入手，寻求它们的规律，然后灵活运用找出的规律解决问题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：

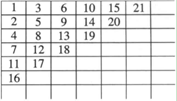    （2010?海安县）将自然数1，2，3，4…按如图那样的顺序排列起来．在最上面的一行中，从左到右第10个数是
    55
    55
    ，在最左边的一列中，从上到下第10个数是
    46
    46
    ．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    如图，将自然数进行排列：
    1）在这个数阵里，用长方形框出二行六个数（图中长方形框仅为示意），如果框出来的六个数的和是192，你知道框出的这六个数中最小的那个数是多少吗？
    2）如果只框到48为止的话，一共可以框出多少个大小不同的和？

    查看答案和解析>>

    科目：小学数学 来源： 题型：

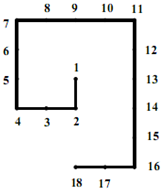    将自然数1、2、3、4^按如图排列：从1开始，下面写2，然后向右转写3、4，然后向上转写5、6、7，依次写下去，这样第一次转弯是2，第2次转弯是4，第3次转弯是7，第4次转弯是11…
    （1）第10次转弯是几？
    （2）第2011次转弯是几？

    查看答案和解析>>

    科目：小学数学 来源： 题型：

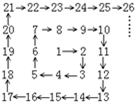    将自然数1，2，3，4…按箭头所指方向顺序排列（如图），依次在2，3，5，7，10…等数的位置处拐弯．
    （1）如果2算作第一次拐弯处，那么第45次拐弯的数是什么？
    （2）从1978到2010的自然数中，恰好在拐弯处的数是什么？

    查看答案和解析>>

    同步练习册答案