

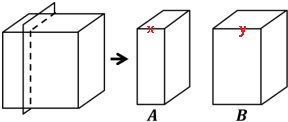
 =
= ;
; =
= ,
,

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:小学数学 来源: 题型:
查看答案和解析>>
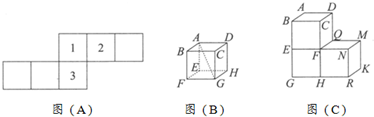
科目:小学数学 来源: 题型:
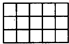 如图,一张长方形硬纸,正好分成15个小正方形.试把它们分成3部分,使每部分有5个小正方形相连,折起来都可以成为一个没有盖的正方体纸盒.请将每部分用不同的阴影表示出来.
如图,一张长方形硬纸,正好分成15个小正方形.试把它们分成3部分,使每部分有5个小正方形相连,折起来都可以成为一个没有盖的正方体纸盒.请将每部分用不同的阴影表示出来.查看答案和解析>>
科目:小学数学 来源: 题型:
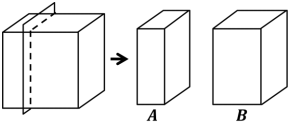
 如图,一个边长是5厘米的正方体,是由125个边长为1厘米的小正方体组成的.P为上底面ABCD的对角线的交点.分别用通过P、E、F三点的平面,P、F、G三点的平面,P、H、G三点的平面,P、H、E三点的平面把正方体切开,则最后剩下的立体图形中包含
如图,一个边长是5厘米的正方体,是由125个边长为1厘米的小正方体组成的.P为上底面ABCD的对角线的交点.分别用通过P、E、F三点的平面,P、F、G三点的平面,P、H、G三点的平面,P、H、E三点的平面把正方体切开,则最后剩下的立体图形中包含查看答案和解析>>
科目:小学数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com