Question

10．AD=8厘米，EC=5厘米，求阴影部分的面积．

Answer 1

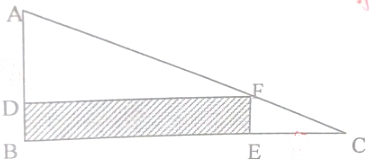
分析 如下图，通过作辅助线，根据长方形的对角线把长方形分成两个完全一样的三角形，三角形AE′F+三角形CD′F+四边形E′FD′G=长方形ABCG面积的一半，三角形ADF+三角形CEF+阴影部分的面积=长方形ABCG面积的一半，由此得：阴影部分的面积等于四边形E′FD′G的面积，根据长方形的面积公式：s=ab，把数据代入公式解答．

解答 解：如图：
S_△AE′F+S_△CD′F+S_四边形E′FD′G=$\frac{1}{2}$S_ABCG，
S_ADF+S_CEF+阴影部分的面积=$\frac{1}{2}$S_ABCG，
所以，阴影部分的面积=四边形E′FD′G的面积=8×5=40（平方厘米），
答：阴影部分的面积是40平方厘米．

点评 此题解答关键是通过作辅助线，利用等量代换的方法进行解答．