

| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 5 |
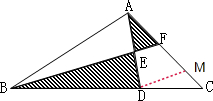
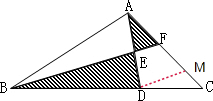
 因为E是AD的中点,所以S△AEF=S△DEF,S△ABE=S△BDE.
因为E是AD的中点,所以S△AEF=S△DEF,S△ABE=S△BDE.| 2 |
| 5 |
| 2 |
| 5 |


 步步高达标卷系列答案
步步高达标卷系列答案科目:小学数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 8 |
查看答案和解析>>
科目:小学数学 来源: 题型:
 如图,P,Q分别是正方形ABCD的边AD和对角线 AC上的点,且PD:AP=4:1,QC:AQ=2:3,如果正方形ABCD的面积为25,那么三角形PBQ的面积是
如图,P,Q分别是正方形ABCD的边AD和对角线 AC上的点,且PD:AP=4:1,QC:AQ=2:3,如果正方形ABCD的面积为25,那么三角形PBQ的面积是查看答案和解析>>
科目:小学数学 来源: 题型:
 在一项射箭比赛中,规定每位运动员能射3支箭,射中了哪一环就得到哪一环上相应的分数,没有射中就不得分.这位运动员用3只支箭刚好射得50分的方式一共有
在一项射箭比赛中,规定每位运动员能射3支箭,射中了哪一环就得到哪一环上相应的分数,没有射中就不得分.这位运动员用3只支箭刚好射得50分的方式一共有查看答案和解析>>
科目:小学数学 来源: 题型:
 如图,灰太狼从A出发,不断往返于AB之间,懒羊羊从C出发按C-E-F-D围绕矩形不断行走.已知AC=80米,CD=EF=120米,CE=DF=30米,BD=100米,灰太狼的速度是5米/秒,懒羊羊的速度是4米/秒,灰太狼从背后第一次追上懒羊羊需要多少秒?
如图,灰太狼从A出发,不断往返于AB之间,懒羊羊从C出发按C-E-F-D围绕矩形不断行走.已知AC=80米,CD=EF=120米,CE=DF=30米,BD=100米,灰太狼的速度是5米/秒,懒羊羊的速度是4米/秒,灰太狼从背后第一次追上懒羊羊需要多少秒?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com