
 ”与“
”与“ ”的积是一个七位数,且它的个位和百万位数字与“学”所代表的数字相同,那么“
”的积是一个七位数,且它的个位和百万位数字与“学”所代表的数字相同,那么“ ”所能代表的两位数共有
”所能代表的两位数共有 ”与“
”与“ ”的积是一个七位数,且它的个位和百万位数字与“学”所代表的数字相同,那么习=1,若习取大于1的数字,则不满足题意,又因为1111×2222=2468642,1111×3333=3702963,1111×4444=4937284,1111×5555=6171605,不符合题意,据此即可解答问题.
”的积是一个七位数,且它的个位和百万位数字与“学”所代表的数字相同,那么习=1,若习取大于1的数字,则不满足题意,又因为1111×2222=2468642,1111×3333=3702963,1111×4444=4937284,1111×5555=6171605,不符合题意,据此即可解答问题. ”所能代表的两位数有21、31、41,一共有3个.
”所能代表的两位数有21、31、41,一共有3个. ”所能代表的两位数共有 3个.
”所能代表的两位数共有 3个.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:小学数学 来源: 题型:

 变为数字
变为数字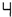 ,我们必须改变3个发光体,即F、C这二个发光体由亮变暗,E这个发光体由暗变亮.
,我们必须改变3个发光体,即F、C这二个发光体由亮变暗,E这个发光体由暗变亮.查看答案和解析>>
科目:小学数学 来源: 题型:

查看答案和解析>>
科目:小学数学 来源: 题型:
 图中“祖冲之杯邀请赛”恰恰代表了1,2,3,4,5,6,7这七个不同的数字,而且每个圆圈内的四个数字之和为15;
图中“祖冲之杯邀请赛”恰恰代表了1,2,3,4,5,6,7这七个不同的数字,而且每个圆圈内的四个数字之和为15;查看答案和解析>>
科目:小学数学 来源: 题型:
| A、2% | B、2.5% |
| C、3% | D、3.5% |
查看答案和解析>>
科目:小学数学 来源: 题型:

查看答案和解析>>
科目:小学数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com