
 ,第三次是第二次的2倍,大、中、小三个球的体积之比是________:________:________.
,第三次是第二次的2倍,大、中、小三个球的体积之比是________:________:________. ,那么第一次溢出水的体积就是小球的体积是1份;第二次把小球取出,把中球沉入水中,可知第二次溢出水的体积就是中球的体积去掉小球的体积是2份,所以中球的体积是3份,第三次取出中球,把小球和大球一起沉入水中.这时第三次是第二次的2倍,可知第三次溢出水的体积就是小球的体积加上大球的体积减去中球的体积是2×2=4份,所以,大球的体积是6份,由以上可以看出:小球的体积、中球的体积、大球的体积的比.
,那么第一次溢出水的体积就是小球的体积是1份;第二次把小球取出,把中球沉入水中,可知第二次溢出水的体积就是中球的体积去掉小球的体积是2份,所以中球的体积是3份,第三次取出中球,把小球和大球一起沉入水中.这时第三次是第二次的2倍,可知第三次溢出水的体积就是小球的体积加上大球的体积减去中球的体积是2×2=4份,所以,大球的体积是6份,由以上可以看出:小球的体积、中球的体积、大球的体积的比. ,可知第二次是第一次的2倍,
,可知第二次是第一次的2倍,

 名校课堂系列答案
名校课堂系列答案科目:小学数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:小学数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:小学数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:小学数学 来源:模拟题 题型:解答题
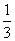 ,第三次溢出的水是第一次的2.5倍。大、中、小三球的体积比是多少?
,第三次溢出的水是第一次的2.5倍。大、中、小三球的体积比是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com