练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
    9．根据各式的规律填空：
    1=12
    1+3=22           
    1+3+5=32
    1+3+5+7=42
    （1）1+3+5+7+9+11+13=72．
    （2）从1开始，20个连续奇数相加的和是202．

    分析 （1）观察图形可知，从1开始的连续奇数的和等于奇数个数的平方，然后计算即可得解；
    （2）连续奇数相加的和是202，可得是从1开始20个连续奇数的和．

    解答 解：（1）1+3+5+7+9+11+13=72；
    （2）观察图形可知，从1开始的连续奇数的和等于奇数个数的平方，
    所以从1开始，20个连续奇数相加的和是202．
    故答案为：（1）7；（2）20．

    点评 此题考查数字的变化规律，找出数字之间的运算规律，利用规律解决问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：解答题

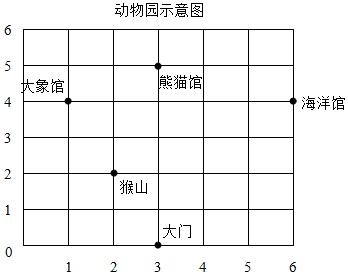    19．如图，如果用（3，0）表示大门的位置，那么，熊猫馆在（3，5）；在图上标出下面场馆的位置飞禽馆（1，1）猩猩馆（0，3）狮虎山（4，3）．

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    20．一个养鸡场星期一收的鸡蛋，16千克装一箱，装了21箱后，还剩下18千克，这个养鸡场星期一收了多少个鸡蛋？

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    17．直接写出下面各题的得数．
    6.8÷0.8=7.5-0.45=4.7+4.3=2÷0.25=6.2÷0.62-1=
    0.75÷1.5=2÷0.2=0.41×4=4.2×60=8+3.2÷0.8=

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    4．“小明体重比爸爸的体重轻$\frac{8}{15}$”这句话中把爸爸的体重看作单位“1”，数量关系式是：爸爸的体重×（1-$\frac{8}{15}$）=小明体重；如果小明的体重是35千克，那么爸爸的体重是75千克．

    查看答案和解析>>

    科目：小学数学 来源： 题型：选择题

    14．一个圆形水池周长是31.4米，在它周围修一条1米宽的水泥路，水泥路面积是（　　）平方米．
    A．34.54B．65.94C．3.14

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    1．图中，正方形的边长是20米．
    （1）请你找出右图中圆的圆心，并用字母O标出圆心；画出图中这个圆的一条直径，并用字母标出来．
    （2）沿这个圆边走一圈要走多少米？
    （3）为这个正方形和圆之间的部分种上草，每平方米要20元，共要多少钱？

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    18．把一张纸分成5份，4份就是这张纸的$\frac{4}{5}$．×．（判断对错）

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    19．盒子里装有3个红球，4个蓝球，5个黄球．从盒子里任意摸出一个小球，摸出黄球的可能性最大，红球的可能性最小．

    查看答案和解析>>

    同步练习册答案