
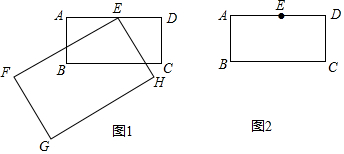
分析 (1)先判断出PE=AE,再判断出∠PEN=∠AEM,进而得到△PEN≌△AEM,即可得出结论;
(2)先判断出PN=CN=$\frac{1}{2}$PC,进而求出PN=CN=$\frac{1}{2}$,再判断出AM=PN,即可得出BM=$\frac{1}{2}$,结论得证;
(3)在直角三角形PEM中,求出PM,再用线段的和差即可得出结论.
解答 解:(1)如图1,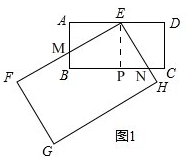 过点E作EP⊥BC,垂足为点P,
过点E作EP⊥BC,垂足为点P,
则四边形ABPE是矩形,
∴PE=AB=1,∠AEP=90°,
∵点E是AD的中点,
∴AE=DE=$\frac{1}{2}$AD=1,
∴PE=AE,
∵∠MEN=∠AEP=90°,
∴∠MEN-∠MEP=∠AEP-∠MEP,
∴∠PEN=∠AEM,
∵PE=AE,∠EPN=∠EAM=90°,
∴△PEN≌△AEM,
∴EM=EN,
(2)由(1)知,△PEN≌△AEM,
∴AM=PN,
∵AM=CN,
∴PN=CN=$\frac{1}{2}$PC,
∵四边形EPCD是矩形,
∴PC=DE=1,PN=CN=$\frac{1}{2}$,
∴AM=PN=$\frac{1}{2}$,BM=AB-AM=$\frac{1}{2}$,
∴AM=BM,
(3)如图2,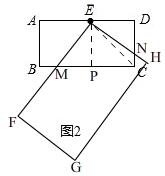 当∠AEF=60°时,
当∠AEF=60°时,
设EF与BC交于M,EH与CD交于N,过点E作EP⊥BC于P,连接EC,
由(1)知,CP=EP=1,AD∥BC,
∴∠EMP=∠AEF=60°,
在Rt△PEM中,PM=$\frac{EP}{tan60°}$=$\frac{\sqrt{3}}{3}$,
∴BM=BP-PM=1-$\frac{\sqrt{3}}{3}$,CM=PC+PM=1+$\frac{\sqrt{3}}{3}$,
∴EF将边BC分成的两条线段的长度为1-$\frac{\sqrt{3}}{3}$,1+$\frac{\sqrt{3}}{3}$.
点评 此题是四边形综合题,主要考查了矩形的性质,全等三角形的判定和性质,解(1)的关键是判断出PE=AE,解(2)的关键是得出PN=CN=$\frac{1}{2}$,解(3)的关键是求出PM.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
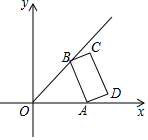 如图,在平面直角坐标系xOy中,点A从点O开始沿x轴的正方向移动,点B在∠xOy平分线上移动,移动中保持AB=2不变,以AB为一边,着AB右侧作矩形ABCD,且BC=1.
如图,在平面直角坐标系xOy中,点A从点O开始沿x轴的正方向移动,点B在∠xOy平分线上移动,移动中保持AB=2不变,以AB为一边,着AB右侧作矩形ABCD,且BC=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在下列有理数运算中,不能借助下面数轴解释的是( )
在下列有理数运算中,不能借助下面数轴解释的是( )| A. | (-3)+(-3)=-6 | B. | (-3)×2=-6 | C. | 2×(-3)=-6 | D. | 3×(-2)=-6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com