
【题目】已知二次函数![]() 的图象与y轴的交点为C,与x轴正半轴的交点为A,且tan∠ACO=
的图象与y轴的交点为C,与x轴正半轴的交点为A,且tan∠ACO=![]() .
.
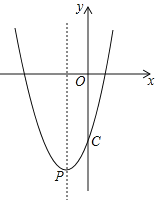
(1)求二次函数的解析式;
(2)P为二次函数图象的顶点,Q为其对称轴上的一点,QC平分∠PQO,求Q点坐标;
(3)是否存在实数![]() 、
、![]() (
(![]() ),当
),当![]() 时,y的取值范围为
时,y的取值范围为![]() ?若存在,直接写在
?若存在,直接写在![]() 、
、![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() ;(2)Q(
;(2)Q(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)
);(3)![]() ,
,![]() .
.
【解析】
试题(1)由tan∠ACO=![]() ,求出OA的值,即可得出A点的坐标;然后把A点的坐标代入
,求出OA的值,即可得出A点的坐标;然后把A点的坐标代入![]() ,求出b的值,即可得出二次函数的解析式.
,求出b的值,即可得出二次函数的解析式.
(2)由Q为抛物线对称轴上的一点,设点Q的坐标为(![]() ,n);然后根据∠OQC=∠CQP、∠CQP=∠OCQ,可得∠OQC=∠OCQ,所以OQ=OC,据此求出n的值,进而得出Q点坐标即可.
,n);然后根据∠OQC=∠CQP、∠CQP=∠OCQ,可得∠OQC=∠OCQ,所以OQ=OC,据此求出n的值,进而得出Q点坐标即可.
(3)根据题意,分三种情况:①当![]() 时;②当
时;②当![]() 时;③当
时;③当![]() 时;然后根据二次函数的最值的求法,求出满足题意的实数
时;然后根据二次函数的最值的求法,求出满足题意的实数![]() 、
、![]() (
(![]() ),当
),当![]() 时,y的取值范围为
时,y的取值范围为![]() 即可.
即可.
试题解析:(1)如图1,连接AC,
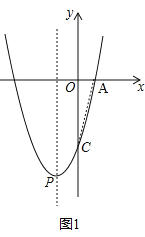 ,
,
∵二次函数![]() 的图象与y轴的交点为C,∴C点的坐标为(0,﹣4),∵tan∠ACO=
的图象与y轴的交点为C,∴C点的坐标为(0,﹣4),∵tan∠ACO=![]() ,∴
,∴![]() ,又∵OC=4,∴OA=1,∴A点的坐标为(1,0),把A(1,0)代入
,又∵OC=4,∴OA=1,∴A点的坐标为(1,0),把A(1,0)代入![]() ,可得0=1+b﹣4,解得b=3,∴二次函数的解析式是:
,可得0=1+b﹣4,解得b=3,∴二次函数的解析式是:![]() ;
;
(2)如图2,
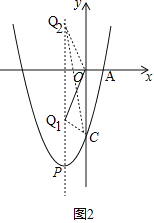 ,
,
∵![]() ,
,
∴抛物线的对称轴是:![]() ,∵Q为抛物线对称轴上的一点,∴设点Q的坐标为(
,∵Q为抛物线对称轴上的一点,∴设点Q的坐标为(![]() ,n),∵抛物线的对称轴平行于y轴,∴∠CQP=∠OCQ,又∵∠OQC=∠CQP,∴∠OQC=∠OCQ,∴OQ=OC,∴
,n),∵抛物线的对称轴平行于y轴,∴∠CQP=∠OCQ,又∵∠OQC=∠CQP,∴∠OQC=∠OCQ,∴OQ=OC,∴![]() ,∴
,∴![]() ,解得n=
,解得n=![]() ,∴Q点坐标是(
,∴Q点坐标是(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
(3)①当![]() 时,二次函数
时,二次函数![]() 单调递减,∵y的取值范围为
单调递减,∵y的取值范围为![]() ,∴
,∴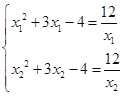 ,由
,由![]() ,解得
,解得![]() =﹣3,﹣2,2,由
=﹣3,﹣2,2,由![]() ,解得
,解得![]() =﹣3,﹣2,2,∵
=﹣3,﹣2,2,∵![]() ,∴
,∴![]() ;
;
②当![]() 时,
时,
Ⅰ、当![]() 时,可得
时,可得![]() ,∵y的取值范围为
,∵y的取值范围为![]() ,
,
∴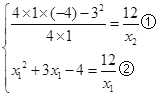 ,由①,可得
,由①,可得![]() ,由②,可得
,由②,可得![]() =﹣3,﹣2,2,∵
=﹣3,﹣2,2,∵![]() ,
,![]() ,∴没有满足题意的
,∴没有满足题意的![]() 、
、![]() ;
;
Ⅱ、当![]() 时,可得
时,可得![]() ,∵y的取值范围为
,∵y的取值范围为![]() ,
,
∴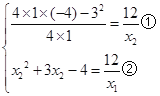 ,解得:
,解得: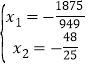 ,∵
,∵![]() ≈﹣1.98﹣1.92=﹣3.9<﹣3,∴没有满足题意的
≈﹣1.98﹣1.92=﹣3.9<﹣3,∴没有满足题意的![]() 、
、![]() .
.
③当![]() 时,二次函数
时,二次函数![]() 单调递增,∵y的取值范围为
单调递增,∵y的取值范围为![]() ,∴
,∴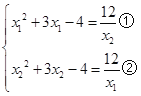 ,①×
,①×![]() ﹣②×
﹣②×![]() ,可得:
,可得:![]() ,∵
,∵![]() ≠0,∴
≠0,∴![]() =0,∴
=0,∴![]() ③,把③代入①,可得:
③,把③代入①,可得:![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,∴没有满足题意的
,∴没有满足题意的![]() 、
、![]() .
.
综上,可得:![]() ,
,![]() ,当
,当![]() 时,y的取值范围为
时,y的取值范围为![]() .
.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
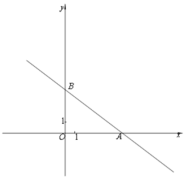
【题目】在平面直角坐标系![]() 中,直线
中,直线![]()
![]() 与
与![]() 轴、
轴、![]() 轴分别交于点A、B如图所示,点
轴分别交于点A、B如图所示,点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() .
.
(1)用含字母![]() 的代数式表示点
的代数式表示点![]() 的坐标;
的坐标;
(2)抛物线y经过点![]() 、
、![]() ,求此抛物线的表达式;
,求此抛物线的表达式;
(3)在第(2)题的条件下,位于第四象限的抛物线上,是否存在这样的点![]() :使
:使![]() ,如果存在,求出点
,如果存在,求出点![]() 的坐标,如果不存在,试说明理由.
的坐标,如果不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
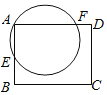
【题目】如图,在矩形ABCD中,过点A的圆O交边AB于点E,交边AD于点F,已知AD=5,AE=2,AF=4.如果以点D为圆心,r为半径的圆D与圆O有两个公共点,那么r的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲杯中盛有m毫升红墨水,乙杯中盛有m毫升蓝墨水,从甲杯中倒出a毫升到乙杯里(0<a<m),搅匀后,又从乙杯倒出a毫升到甲杯里,则这时( )
A. 甲杯中混入的蓝墨水比乙杯中混入的红墨水少
B. 甲杯中混入的蓝墨水比乙杯中混入的红墨水多
C. 甲杯中混入的蓝墨水和乙杯中混入的红墨水相同
D. 甲杯中混入的蓝墨水与乙杯中混入的红墨水多少关系不定
查看答案和解析>>
科目:初中数学 来源: 题型:
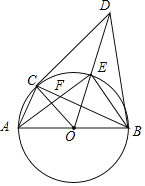
【题目】如图,AB为⊙O的直径,BC为⊙O的弦,过O点作OD⊥BC,交⊙O的切线CD于点D,交⊙O于点E,连接AC、AE,且AE与BC交于点F.
(1)连接BD,求证:BD是⊙O的切线;
(2)若AF:EF=2:1,求tan∠CAF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
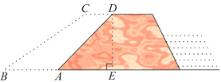
【题目】为做好汉江防汛工作,防汛指挥部决定对一段长为2500m重点堤段利用沙石和土进行加固加宽.专家提供的方案是:使背水坡的坡度由原来的1:1变为1:1.5,如图,若CD∥BA,CD=4米,铅直高DE=8米.
(1)求加固加宽这一重点堤段需沙石和土方数是多少?
(2)某运输队承包这项沙石和土的运送工程,根据施工方计划在一定时间内完成,按计划工作5天后,增加了设备,工效提高到原来的1.5倍,结果提前了5天完成任务,问按原计划每天需运送沙石和土多少m3?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)某种电子产品共![]() 件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为
件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为![]() .
.
(1)该批产品有正品 件;
(2)如果从中任意取出![]() 件,利用列表或树状图求取出
件,利用列表或树状图求取出![]() 件都是正品的概率.
件都是正品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
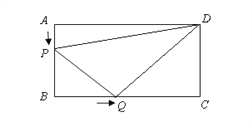
【题目】如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
(1)当PB=2厘米时,求点P移动多少秒?
(2)t为何值时,△PBQ为等腰直角三角形?
(3)求四边形PBQD的面积,并探究一个与计算结果有关的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
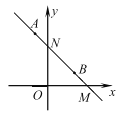
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,若抛物线
,若抛物线![]() 与直线
与直线![]() 有两个不同的交点,其中一个交点在线段
有两个不同的交点,其中一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),另一个交点在线段
两个端点),另一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),则
两个端点),则![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com