Question

【题目】如图，△ABD是等腰三角形，AB=AD，将△ABD沿BD翻折得△CBD，点P是线段BD上一点，
（1）如图1，连接PA、PC，求证：CP=AP；

（2）如图2，连接PA，若∠BAP=90°时，作∠DPF=45°，线段PF交线段CD于F，求证：AD=AP+DF；

（3）如图3，∠ABD=30°，连接AP并延长交CD于M，若∠BAM=90°，在BD上取一点Q，且DQ=3BQ，连BM、CQ，当BM= 时，求CQ的长．

Answer 1

【答案】
（1）

证明：由翻折有，AD=CD，∠ADP=∠CDP，

在△ADP和△CDP中，

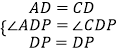
∴△ADP≌△CDP，

∴CP=AP

（2）

证明：连接PC，由（1）有，AP=CP，

由翻折有∠BCP=∠BAP=90°，

∴∠CBP+∠BPC=90°，

∵AD=AB=CB=CD，

∴∠CBP=∠CDP，

∴∠CDP+∠BPC=90°，

∵∠DPF=45°，

∴∠BPC+∠CPF=135°，

∴∠CPF=∠CDP+45°，

∵∠CFP=∠CDP+∠BPF=∠CDP+45°，

∴∠CPF=∠CFP，

∴CP=CF，

∴AD=CB=CF+FD=CP+FD=AP+FD

（3）

证明：如图，连接AQ，AC，

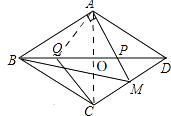
由（1）有，AQ=CQ，AP=CP，由翻折有AB=BC，AD=CD，

∵AB=AD，

∴AB=BC=CD=AD，

∴四边形ABCD是菱形，

∴AC⊥BD，OB=OD，OA=OC，∠BAD=120°，

∵DQ=3BQ，

∴BQ=OQ，

∴四边形CPAQ也是菱形，

∵∠BAM=90°，∠BAD=120°，

∴∠BAQ=∠DAM=30°，

∴∠ABD=∠CBD=∠ADB=∠CDB=30°，

∵∠ADM=60°，

∴∠AMD=90°，

∵△ACD等边三角形，

∴CD=2DM．

设DM=x，

∴CD=AD=AB=2DM=2x，AM= x，

在Rt△ABM中，BM= ，

∴AB2+AM2=BM2，

∴（2x）2+（ x）2=（ ）2，

∴x= 或x=﹣ （舍），

在RT△AOB中，∠ABD=30°，

∴OA= AB=x，OB= x，

∵OQ=BQ= OB= x，

在RT△AOQ中，AQ= = x= ，

∴CQ=AQ= ．

【解析】（1）由翻折得到条件，直接判断出△ADP≌△CDP，即可；（2）由（1）结论CP=AP，用三角形的外角等于与它不相邻的两内角的和及平角的定义判断出∠CPF=∠CFP，得到CP=CF，即可；（3）由（1）的结论判断出四边形ABCD是菱形，继而判断出四边形AQCP也是菱形，利用勾股定理求出MN即可．
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识，掌握等腰三角形的两个底角相等（简称：等边对等角），以及对等腰三角形的判定的理解，了解如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等．