
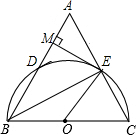
 如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,过点E作半圆O的切线,交AB于M,连接BE.
如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,过点E作半圆O的切线,交AB于M,连接BE.分析 (1)由直径所对的圆周角是直角,切线垂直于过切点的半径,然后利用互余得出结论;
(2)由切割线定理即可;
(3)利用勾股定理和等角的同名三角函数值相等,建立方程即可.
解答 解:(1)∵BC为直径,
∴∠BEC=∠AEB=90°,
∴∠AEM+∠BEM=90°,
∵EM为⊙O的切线,
∴∠MEO=90°,
∴∠BEM+∠OEB=90°,
∴∠AEM=∠OEB,
∵OB=OE,
∴∠OEB=∠EBC=∠AEM;
(2)由割线定理得,AE×AC=AD×AB,
∵AE=AD,
∴AB=AC;
(3)∵AB=AC,AD=AE
∴AB-AD=AC-AE,
∴BD=CE=4,
在Rt△BEC中,BC=2BO=4$\sqrt{5}$,CE=4,
∴BE=$\sqrt{B{C}^{2}-C{E}^{2}}$=8,
设AE=x,则AB=AC=4+x,
在Rt△BEA中,AB2=AE2+BE2,
∴(4+x)2=x2+82,
∴x=6,
∴AE=6,
∵EM为切线,
∴∠OEM=90°,
∵OB=OE,
∴∠OBE=∠CEB,
∵∠EBC=∠AEM
∴∠AEM=∠EBC,
∴sin∠AEM=sin∠EBC=$\frac{4}{4\sqrt{5}}$=$\frac{AM}{AE}$,
∴AM=$\frac{4}{4\sqrt{5}}$×AE=$\frac{\sqrt{5}}{5}$×6=$\frac{6\sqrt{5}}{5}$
点评 此题是圆的综合题,主要考查了直径所对的圆周角是直角,切线垂直于过切点的半径,切割线定理,勾股定理,解本题的关键是用勾股定理的结论表示相关相等(设AE=x,则AB=AC=4+x,),再另一个直角三角形中用勾股定理建立方程.


科目:初中数学 来源: 题型:解答题
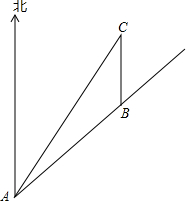 如图,一条笔直的公路经过两个城镇A和B,为了改善居住条件,当地要建设一个新城镇C,已知新城镇C在城镇A的北偏东30°方向距城镇A 8km处,且位于城镇B的正北方向,已知AB=4$\sqrt{2}$km,求新城镇C到公路的距离.(结果保留到0.1km,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,$\sqrt{6}$≈2.45)
如图,一条笔直的公路经过两个城镇A和B,为了改善居住条件,当地要建设一个新城镇C,已知新城镇C在城镇A的北偏东30°方向距城镇A 8km处,且位于城镇B的正北方向,已知AB=4$\sqrt{2}$km,求新城镇C到公路的距离.(结果保留到0.1km,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,$\sqrt{6}$≈2.45)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
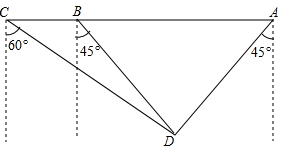 如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向上,海监船航行到B处时望见渔船D在南偏东45°方向上,又航行了半小时到达C处,望见渔船D在南偏东60°方向上,若海监船的速度为40海里/时,求A,B之间的距离.(结果保留根号)
如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向上,海监船航行到B处时望见渔船D在南偏东45°方向上,又航行了半小时到达C处,望见渔船D在南偏东60°方向上,若海监船的速度为40海里/时,求A,B之间的距离.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$-$\sqrt{3}$=2 | B. | a$\sqrt{c}$+b$\sqrt{c}$=a+b$\sqrt{c}$ | C. | 5$\sqrt{a}$+$\frac{1}{2}$$\sqrt{a}$=5+$\frac{1}{2}$$\sqrt{a}$ | D. | $\frac{1}{3}$$\sqrt{3a}$-$\frac{1}{4}$$\sqrt{3a}$=$\frac{1}{12}$$\sqrt{3a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
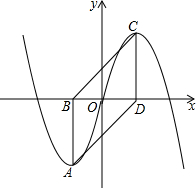 如图,在平面直角坐标系中,过抛物线y=a(x+1)2-2(x≤0,a为常数)的顶点A作AB⊥x轴于点B,过抛物线y=-a(x-1)2+2(x≥0,a为常数)的顶点C作CD⊥x轴于点D,连结AD、BC.则四边形ABCD的面积为4.
如图,在平面直角坐标系中,过抛物线y=a(x+1)2-2(x≤0,a为常数)的顶点A作AB⊥x轴于点B,过抛物线y=-a(x-1)2+2(x≥0,a为常数)的顶点C作CD⊥x轴于点D,连结AD、BC.则四边形ABCD的面积为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com