
【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=4,CE= ![]() ,则△ABC的面积为( )
,则△ABC的面积为( ) 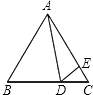
A.8 ![]()
B.15
C.9 ![]()
D.12 ![]()
【答案】C
【解析】解:∵△ABC是等边三角形,∠ADE=60°, ∴∠B=∠C=∠ADE=60°,AB=BC,
∵∠ADB=∠DAC+∠C,∠DEC=∠ADE+∠DAC,
∴∠ADB=∠DEC,
∴△ABD∽△DCE,
∴ ![]() ,
,
∵BD=4,CE= ![]() ,
,
设AB=x,则DC=x﹣4,
∴ ![]() ,
,
∴x=6,
∴AB=6,
过点A作AF⊥BC于F,
在Rt△ABF中,AF=ABsin60°=6× ![]() =3
=3 ![]() ,
,
∴S△ABC= ![]() BCAF=
BCAF= ![]() ×6×3
×6×3 ![]() =9
=9 ![]() .
.
故选C.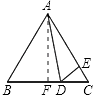
首先由△ABC是等边三角形,可得∠B=∠C=∠ADE=60°,又由三角形外角的性质,求得∠ADB=∠DEC,即可得△ABD∽△DCE,又由BD=4,CE= ![]() ,根据相似三角形的对应边成比例,即可求得AB的长,则可求得△ABC的面积.
,根据相似三角形的对应边成比例,即可求得AB的长,则可求得△ABC的面积.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小国同学的父亲参加旅游团到某地旅游,准备买某种礼物送给小国.据了解,沿旅游线路依次有A、B、C三个地点可以买到此种礼物,其质量相当,价格各不相同,但不知哪家更便宜.由于时间关系,随团旅游车不会掉头行驶.
(1)若到A处就购买,写出买到最低价格礼物的概率;
(2)小国同学的父亲认为,如果到A处不买,到B处发现比A处便宜就马上购买,否则到C处购买,这样更有希望买到最低价格的礼物.这个想法是否正确?试通过树状图分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
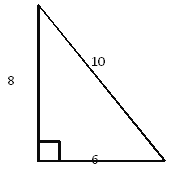
【题目】如图,已知一个边长分别为6、8、10的直角三角形,请设计出一个有一条边长为8的直角三角形,使这两个直角三角形能够拼成一个等腰三角形.
(1)画出4种不同拼法(周长不等)的等腰三角形;
(2)分别求出4种不同拼法的等腰三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,飞机沿水平方向(A、B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低.就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行距离 (因安全因素,飞机不能飞到山顶的正上方N处才测飞行距离),请设计一个求距离MN的方案,要求: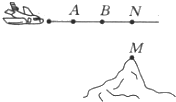
(1)指出需要测量的数据(用字母表示,并在图中标出);
(2)用测出的数据写出求距离MN的步骤.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地保护美丽如画的邛海湿地,西昌市污水处理厂决定先购买A,B两种型号的污水处理设备共20台,对邛海湿地周边污水进行处理.每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640 t,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1 080 t.
(1)求A,B两种型号的污水处理设备每周每台分别可以处理污水多少吨.
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4 500 t,请你列举出所有购买方案,并指出哪种方案所需资金最少,最少是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
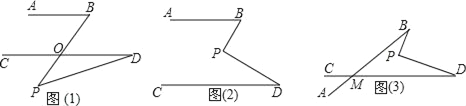
【题目】(1)如图(1),AB∥CD,点P在AB,CD外部,若∠B=50°,∠D=25°,则∠BPD= °
(2)如图(2),AB∥CD,点P在AB,CD内部,则∠B,∠D,∠BPD之间有何数量关系?证明你的结论.
(3)在图(2)中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图(3),若∠BPD=90°,∠BMD=40°,求∠B+∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
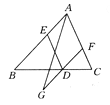
【题目】如图所示,已知D,E,F分别在△ABC的边BC,AB,AC上,且DE∥AF,DE=AF,将FD延长至G,使FG=2DF,连接AG,则ED,AG互相平分吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
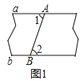
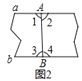


A. 如图1,展开后测得∠1=∠2
B. 如图2,展开后测得∠1=∠2且∠3=∠4
C. 如图3,测得∠1=∠2
D. 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com