
 如图△PAB中,PA=PB,PB为⊙O的切线,B为切点,连接OP交AB于点C,延长BO与⊙O交于点D、与PA的延长线交于点E
如图△PAB中,PA=PB,PB为⊙O的切线,B为切点,连接OP交AB于点C,延长BO与⊙O交于点D、与PA的延长线交于点E分析 (1)连接OA,根据切线的性质得到∠PAO=90°,证明△PBO≌△PAO,根据全等三角形的性质得到∠PBO=∠PAO=90°,证明结论;
(2)连接AD,设OC=x,根据正切的概念用x表示出BC、AD、OB,根据相似三角形的性质求出BE、PE,根据正弦的概念计算即可.
解答 证明:(1)连接OA,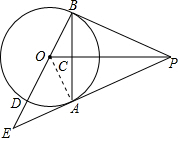
∵PA为⊙O的切线,
∴∠PAO=90°,
∵OA=OB,OP⊥AB,
∴BC=CA,PB=PA,
在△PBO和△PAO中,
$\left\{\begin{array}{l}{OA=OB}\\{PB=PA}\\{OP=OP}\end{array}\right.$,
∴△PBO≌△PAO,
∴∠PBO=∠PAO=90°,即PA与⊙O相切;
(2)连接AD,
∵tan∠ABE=$\frac{1}{2}$,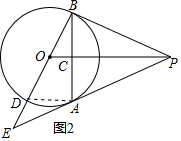
∴设OC=x,BC=CA=2x,AD=2OC=2x,OB=OD=$\sqrt{5}$x,
∵∠ABE=∠OPB,
∴tan∠OPB=$\frac{1}{2}$,
∴CP=4x,OP=x+4x=5x,
∵△ADE∽△POE,
∴DE=$\frac{{2\sqrt{5}}}{3}$x,BE=$\frac{{8\sqrt{5}}}{3}$x,BP=$2\sqrt{5}$x,PE=$\frac{10\sqrt{5}}{3}$x,
∴sinE=$\frac{BP}{PE}$=$\frac{3}{5}$.
点评 本题考查的是切线的判定和性质、正切的概念、相似三角形的判定和性质,掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ±$\frac{1}{5}$是$\frac{1}{25}$的平方根 | B. | 81的平方根是9 | ||
| C. | 0.04的算术平方根是0.2 | D. | -27的立方根是-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
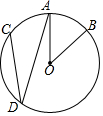 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )| A. | 15° | B. | 20° | C. | 30° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
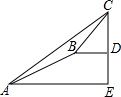 这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5$\sqrt{5}$米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5$\sqrt{5}$米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )| A. | 7米 | B. | 7.2米 | C. | 9.7米 | D. | 15.5米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
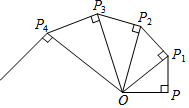 如图OP=1,过P作PP1⊥OP,得$O{P_1}=\sqrt{2}$;再过P1作PP2⊥OP1且PP2=1,得$O{P_2}=\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得:OP3=2;…依此法继续作下去,得OP2014=$\sqrt{2015}$.
如图OP=1,过P作PP1⊥OP,得$O{P_1}=\sqrt{2}$;再过P1作PP2⊥OP1且PP2=1,得$O{P_2}=\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得:OP3=2;…依此法继续作下去,得OP2014=$\sqrt{2015}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com