
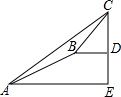
 这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5$\sqrt{5}$米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5$\sqrt{5}$米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )| A. | 7米 | B. | 7.2米 | C. | 9.7米 | D. | 15.5米 |
分析 作BF⊥AE于F,则FE=BD=6米,DE=BF,设BF=x米,则AF=2x米,在Rt△ABF中,由勾股定理得出方程,解方程求出DE=BF=5米,AF=10米,得出AE的长度,在Rt△ACE中,由三角函数求出CE,计算即可.
解答 解: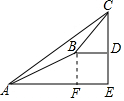 作BF⊥AE于F,
作BF⊥AE于F,
则FE=BD=6米,DE=BF,
∵斜面AB的坡度i=1:2,
∴AF=2BF,
设BF=x米,则AF=2x米,
在Rt△ABF中,由勾股定理得:x2+(2x)2=(5$\sqrt{5}$)2,
解得:x=5,
∴DE=BF=5米,AF=10米,
∴AE=AF+FE=16米,
在Rt△ACE中,CE=AE•tan37°≈16×0.75=12米,
∴CD=CE-DE=12米-5米=7米,
故选:A.
点评 本题考查了解直角三角形的应用、勾股定理、三角函数,掌握锐角三角函数的定义、由勾股定理得出方程是解决问题的关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
 如图△PAB中,PA=PB,PB为⊙O的切线,B为切点,连接OP交AB于点C,延长BO与⊙O交于点D、与PA的延长线交于点E
如图△PAB中,PA=PB,PB为⊙O的切线,B为切点,连接OP交AB于点C,延长BO与⊙O交于点D、与PA的延长线交于点E查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是某副食品公司销售糖果的总利润y(元)与销售量x(千克)之间的函数图象(总利润=总销售额-总成本),该公司想通过“不改变总成本,提高糖果售价”的方案解决销售不佳的现状,下面给出的四个图象,虚线均表示新的销售方案中总利润与销售量之间的函数图象,则能反映该公司改进方案的是( )
如图,是某副食品公司销售糖果的总利润y(元)与销售量x(千克)之间的函数图象(总利润=总销售额-总成本),该公司想通过“不改变总成本,提高糖果售价”的方案解决销售不佳的现状,下面给出的四个图象,虚线均表示新的销售方案中总利润与销售量之间的函数图象,则能反映该公司改进方案的是( )| A. | 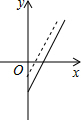 | B. | 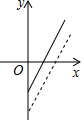 | C. | 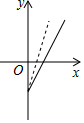 | D. | 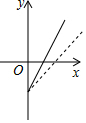 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
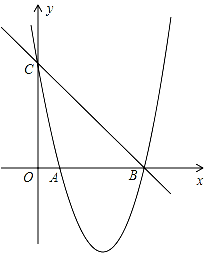 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
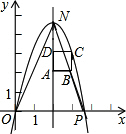 如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=-x2+bx+c经过原点O和点P,已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).
如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=-x2+bx+c经过原点O和点P,已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:
随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:| 数据段 | 频数 | 频率 |
| 30-40 | 10 | 0.05 |
| 40-50 | 36 | c |
| 50-60 | a | 0.39 |
| 60-70 | b | d |
| 70-80 | 20 | 0.10 |
| 总计 | 200 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com