
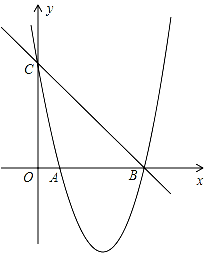
 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).分析 (1)利用待定系数法直接求出直线BC和抛物线解析式;
(2)先判断出点Q的位置,即可得出坐标;
(3)利用平行于y轴的直线上的两点之间的距离确定出函数函数关系式即可确定出最大值.
解答 解:(1)设直线BC的解析式为y=kx+b,
∵B(5,0),C(0,5),
∴$\left\{\begin{array}{l}{5k+b=0}\\{b=5}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$,
∴直线BC的解析式为y=-x+5;
∵抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),与y轴交于点C(0,5),
∴$\left\{\begin{array}{l}{25+5b+c=0}\\{c=5}\end{array}\right.$,
∴$\left\{\begin{array}{l}{b=-6}\\{c=5}\end{array}\right.$,
∴抛物线的解析式为y=x2-6x+5;
(2)如图1,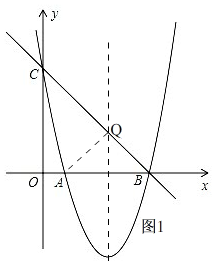
∵点A,B是抛物线y=x2-6x+5与x轴的交点,
∴点A,B关于抛物线y=x2-6x+5的对称轴x=3对称,
∵抛物线的对称轴上的点Q,使得△QAC的周长最小,
∴点Q就是抛物线的对称轴与直线BC的交点,
∴Q(3,2);
(3)如图2,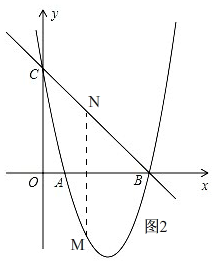
∵抛物线的解析式为y=x2-6x+5;
∴A(1,0),B(5,0),
设点M(m,m2-6m+5)(1<m<5),
∴N(m,-m+5),
∴MN=-m+5-(m2-6m+5)
=-m2+5m=-(m-$\frac{5}{2}$)2+$\frac{25}{4}$,
∴当m=$\frac{5}{2}$时,MN最大是$\frac{25}{4}$.
点评 此题是二次函数综合题,主要考查了待定系数法,函数极值的确定,解(1)的关键是掌握待定系数法确定函数解析式,解(2)的关键是利用对称点确定三角形周长最小时的点Q的位置,解(3)的关键是确定出MN的函数关系式.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
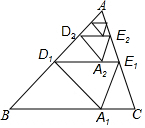 如图,对△ABC纸片进行如下操作:
如图,对△ABC纸片进行如下操作:| A. | $\frac{3}{2}$ | B. | $\frac{7}{4}$ | C. | $\frac{13}{8}$ | D. | $\frac{31}{16}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
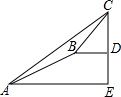 这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5$\sqrt{5}$米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5$\sqrt{5}$米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )| A. | 7米 | B. | 7.2米 | C. | 9.7米 | D. | 15.5米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 队名 | 比赛场次 | 胜场 | 负场 | 积分 |
| A | 16 | 12 | 4 | 28 |
| B | 16 | 10 | 6 | 26 |
| C | 16 | 8 | 8 | 24 |
| D | 16 | 0 | 16 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
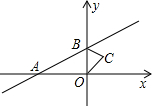 如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-4,-3)或(2,3).
如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-4,-3)或(2,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com