
分析 首先把括号内的分式通分相加,把除法转化为乘法,计算乘法即可化简,然后化简x的值,代入求解即可.
解答 解:原式=[$\frac{2-2x}{x+1}$+x-1]÷$\frac{x(x-1)}{x+1}$
=$\frac{2-2x+{x}^{2}-1}{x+1}$•$\frac{x+1}{x(x-1)}$
=$\frac{{x}^{2}-2x+1}{x(x-1)}$
=$\frac{(x-1)^{2}}{x(x-1)}$
=$\frac{x-1}{x}$.
当x=tan30°=$\frac{\sqrt{3}}{3}$时,原式=$\frac{\frac{\sqrt{3}}{3}-1}{\frac{\sqrt{3}}{3}}$=1-$\sqrt{3}$.
点评 本题考查了分式的化简求值,正确对所求的分式进行通分、约分是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图△PAB中,PA=PB,PB为⊙O的切线,B为切点,连接OP交AB于点C,延长BO与⊙O交于点D、与PA的延长线交于点E
如图△PAB中,PA=PB,PB为⊙O的切线,B为切点,连接OP交AB于点C,延长BO与⊙O交于点D、与PA的延长线交于点E查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是某副食品公司销售糖果的总利润y(元)与销售量x(千克)之间的函数图象(总利润=总销售额-总成本),该公司想通过“不改变总成本,提高糖果售价”的方案解决销售不佳的现状,下面给出的四个图象,虚线均表示新的销售方案中总利润与销售量之间的函数图象,则能反映该公司改进方案的是( )
如图,是某副食品公司销售糖果的总利润y(元)与销售量x(千克)之间的函数图象(总利润=总销售额-总成本),该公司想通过“不改变总成本,提高糖果售价”的方案解决销售不佳的现状,下面给出的四个图象,虚线均表示新的销售方案中总利润与销售量之间的函数图象,则能反映该公司改进方案的是( )| A. | 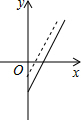 | B. | 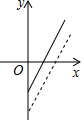 | C. | 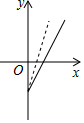 | D. | 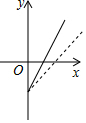 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
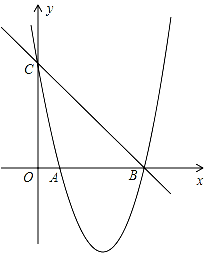 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 若将直尺的0cm刻度线与半径为5cm的量角器的0°线对齐,并让量角器沿直尺的边缘无滑动地滚动,则直尺上的10cm刻度线对应量角器上的度数约为115°.(保留π)
若将直尺的0cm刻度线与半径为5cm的量角器的0°线对齐,并让量角器沿直尺的边缘无滑动地滚动,则直尺上的10cm刻度线对应量角器上的度数约为115°.(保留π)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com