
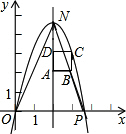 ��ͼ����ֱ������ϵ�У���P�������ǣ�n��0����n��0����������y=-x2+bx+c����ԭ��O�͵�P����֪������ABCD����������ΪA��2��2����B��3��2����D��2��3����
��ͼ����ֱ������ϵ�У���P�������ǣ�n��0����n��0����������y=-x2+bx+c����ԭ��O�͵�P����֪������ABCD����������ΪA��2��2����B��3��2����D��2��3�������� ��1����ԭ���P��������������߽���ʽ�����b��c�������������߽���ʽ����Ϊ����ʽ�������Գ�������ֵ��
��2����n�ɱ�ʾ�������ߵĽ���ʽ���������䶥�����꣬����y=x2������֤���ɣ�
��3������n��ʾ��N�����꣬��ɱ�ʾ��N��x��ľ����OP�ij����ɱ�ʾ����NPO��������ɵõ�����n�ķ��̣������n��ֵ��
��4���ֱ��A��B��C��D��������������߽���ʽ�����n��ֵ��������n��ȡֵ��Χ��
��� �⣺
��1����n=4ʱ����P��4��0����
��������y=-x2+bx+c����ԭ��O�͵�P��
��$\left\{\begin{array}{l}{c=0}\\{-16+4b=0}\end{array}\right.$�����$\left\{\begin{array}{l}{b=4}\\{c=0}\end{array}\right.$��
�������߽���ʽΪy=-x2+4x=-��x-2��2+4��
�������߶Գ���Ϊֱ��x=2��
��-1��0��
�൱x=2ʱ��y�����ֵ4��
��2����O��P��������������߽���ʽ�ɵ�$\left\{\begin{array}{l}{c=0}\\{-{n}^{2}+bn=0}\end{array}\right.$�����$\left\{\begin{array}{l}{b=n}\\{c=0}\end{array}\right.$��
�������߽���ʽΪy=-x2+nx=-��x-$\frac{n}{2}$��2+$\frac{{n}^{2}}{4}$��
�������߶�������Ϊ��$\frac{n}{2}$��$\frac{{n}^{2}}{4}$����
��y=x2�У���x=$\frac{n}{2}$ʱ��y=$\frac{{n}^{2}}{4}$��
�������ߵĶ����ں���y=x2��ͼ���ϣ�
��3����y=-x2+nx�У���x=2ʱ��y=2n-4��
��N��������2��2n-4����
��N��x��ľ���Ϊ|2n-4|=2|n-2|��
��P��n��0����
��OP=n��
��S��NPO=$\frac{1}{2}$n��2|n-2|=n|n-2|��
����NPO�����Ϊ1ʱ������n|n-2|=1��
��n=2ʱ��N��P�غϣ���������
��n��2ʱ����n2-2n=1�����n=1+$\sqrt{2}$��n=1-$\sqrt{2}$����ʱnС��2����ȥ����
��0��n��2ʱ����2n-n2=1�����n1=n2=1��
���Ͽ�֪��n��ֵΪ1+$\sqrt{2}$��1ʱ����NPO�����Ϊ1��
��4���������߽���ʽΪy=-x2+nx��
�൱��A��2��2��ʱ������ɵ�2=-4+2n�����n=3��
ͬ���������߹�Bʱ�����n=$\frac{11}{3}$���������߹���Cʱ�����n=4���������߹���Dʱ�����n=$\frac{7}{2}$��
��n��ȡֵ��ΧΪ3��n��4��
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ���������κ��������ʡ������ε����������ͼ���ϵ��������������������˼���֪ʶ���ڣ�1����ע�����ϵ������Ӧ�ò��裬�ڣ�2������n��ʾ�����������ǽ���Ĺؼ����ڣ�3������N�������ʾ����NPO������ǽ���Ĺؼ����ڣ�4���зֱ���ù�ÿ����ʱ��n��ֵ�ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
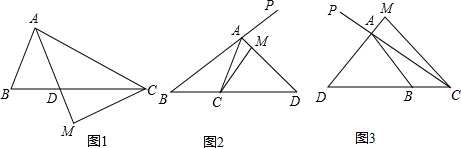
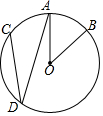 ��ͼ���ڡ�O�У�$\widehat{AB}$=$\widehat{AC}$����AOB=40�㣬���ADC�Ķ����ǣ�������
��ͼ���ڡ�O�У�$\widehat{AB}$=$\widehat{AC}$����AOB=40�㣬���ADC�Ķ����ǣ�������| A�� | 15�� | B�� | 20�� | C�� | 30�� | D�� | 40�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
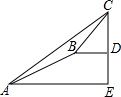 �����ѧʵ�����ϣ�ͬѧ���д���CD�߶ȵ��ۺ�ʵ�������ͼ���ڵ�A�����ֱ���ڵ���Ĵ�������C������Ϊ37�㣬Ȼ������ͬһ�����б��AB����5$\sqrt{5}$�����¶�B����Ȼ������ˮƽ��������6���������ŵ�D����б��AB���¶�i=1��2��ͨ��������Ĵ�ֱ�߶�h��ˮƽ����l�ıȽ����¶ȣ���tan��ֵ����Ϊб����ˮƽ��нǣ�����ô����CD�ĸ߶�ԼΪ���ο����ݣ�sin37���0.6��cos37���0.8��tan37���0.75����������
�����ѧʵ�����ϣ�ͬѧ���д���CD�߶ȵ��ۺ�ʵ�������ͼ���ڵ�A�����ֱ���ڵ���Ĵ�������C������Ϊ37�㣬Ȼ������ͬһ�����б��AB����5$\sqrt{5}$�����¶�B����Ȼ������ˮƽ��������6���������ŵ�D����б��AB���¶�i=1��2��ͨ��������Ĵ�ֱ�߶�h��ˮƽ����l�ıȽ����¶ȣ���tan��ֵ����Ϊб����ˮƽ��нǣ�����ô����CD�ĸ߶�ԼΪ���ο����ݣ�sin37���0.6��cos37���0.8��tan37���0.75����������| A�� | 7�� | B�� | 7.2�� | C�� | 9.7�� | D�� | 15.5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
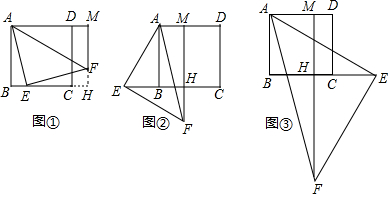
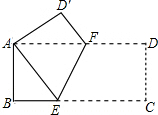 ��ͼ���ھ���ABCD�У�AB=8��BC=16��������ABCD��EF�۵���ʹ��C���A�غϣ����ۺ�EF�ij�Ϊ4$\sqrt{5}$��
��ͼ���ھ���ABCD�У�AB=8��BC=16��������ABCD��EF�۵���ʹ��C���A�غϣ����ۺ�EF�ij�Ϊ4$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| Ų�����������ţ� | 2 | 3 | 4 | 5 | 6 | �� |
| ���÷��� | 5 | 11 | 19 | 29 | 41 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y1��y3��y2 | B�� | y3��y2��y1 | C�� | y2��y3��y1 | D�� | y1��y2��y3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com