

���� ��1�����ö������깫ʽ���г����̼��ɽ�����⣮
��2����BC��y�ᣬB��0��-4�������C����ΪC��m��-4��������m��0��������L����-4=am2+2��a-1��m-4����ã�m=$\frac{2}{a}$-2���ɵõ�C���꣬��Ϊ��A���E����L�ĶԳ���x=$\frac{1}{a}$-1�Գƣ�A��-2��0�������E�������ǣ�n��0��������n��0�����ɵ�$\frac{1}{a}$-1-��-2��=n-��$\frac{1}{a}$-1������� n=$\frac{2}{a}$���ɴ˼��������E���꣮
��3����������S����OBCD=4•|$\frac{2}{a}$-2|=4���ɵ�|$\frac{2}{a}$-2|=1�����������ٵ�����OBCD��y���Ҳ�ʱ���ڵ�����OBCD��y�����ʱ���ֱ���⼴�ɣ�
��4����ͼ���֪����AB��BD��ʱ����A��ֱ��BD��ľ������
��� �⣺��1��������L�ĶԳ�����x=-$\frac{2��a-1��}{2a}$����x=$\frac{1}{a}$-1��
�ߵ�x=2ʱ��Lȡ����͵㣬��$\frac{1}{a}$-1=2��
��a=$\frac{1}{3}$��
��L�Ľ���ʽΪ��y=$\frac{1}{3}$x2-$\frac{4}{3}$x-4��
��2������L�ϣ���BC��y�ᣬB��0��-4����
�����C����ΪC��m��-4��������m��0��������L��
-4=am2+2��a-1��m-4����ã�m=$\frac{2}{a}$-2��
���C�������ǣ�$\frac{2}{a}$-2��-4����
�ߵ�A���E����L�ĶԳ���x=$\frac{1}{a}$-1�Գƣ�A��-2��0����
���E�������ǣ�n��0��������n��0����
��$\frac{1}{a}$-1-��-2��=n-��$\frac{1}{a}$-1������� n=$\frac{2}{a}$��
���E�������ǣ�$\frac{2}{a}$��0����
��3����S����OBCD=4•|$\frac{2}{a}$-2|=4��
��|$\frac{2}{a}$-2|=1��
������OBCD��y���Ҳ�ʱ��0��a��1����$\frac{2}{a}$-2=1�����a=$\frac{2}{3}$��
������OBCD��y�����ʱ��a��1����$\frac{2}{a}$-2=-1�����a=2��
��4����ͼ���֪����AB��BD��ʱ����A��ֱ��BD��ľ������������ΪAB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$��
���� ���⿼����κ����ۺ��⡢�������깫ʽ�����ε����ʡ�����ϵ������֪ʶ������Ĺؼ���ѧ�ṹ�����̽�����⣬���������ѧ֪ʶ��ѧ���÷������۵�˼��˼�����⣬ע�ⲻ��©�⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ʵ��a��b�������ϵ�λ����ͼ������$\sqrt{��a-b��^{2}}$-$\frac{a��a+b��}{|a+b|}$�Ľ��Ϊ��������
ʵ��a��b�������ϵ�λ����ͼ������$\sqrt{��a-b��^{2}}$-$\frac{a��a+b��}{|a+b|}$�Ľ��Ϊ��������| A�� | b | B�� | -b | C�� | -2a+b | D�� | 2a-b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
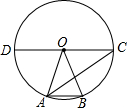 ��ͼ���ڡ�O�У�CD��ֱ������A����B�ڡ�O�ϣ�����OA��OB��AC��AB������AOB=40�㣬CD��AB�����BAC�Ĵ�СΪ��������
��ͼ���ڡ�O�У�CD��ֱ������A����B�ڡ�O�ϣ�����OA��OB��AC��AB������AOB=40�㣬CD��AB�����BAC�Ĵ�СΪ��������| A�� | 30�� | B�� | 35�� | C�� | 40�� | D�� | 70�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ij��ʳƷ��˾�����ǹ���������y��Ԫ����������x��ǧ�ˣ�֮��ĺ���ͼ��������=�����۶�-�ܳɱ������ù�˾��ͨ�������ı��ܳɱ�������ǹ��ۼۡ��ķ���������۲��ѵ���״������������ĸ�ͼ�����߾���ʾ�µ����۷�������������������֮��ĺ���ͼ�����ܷ�ӳ�ù�˾�Ľ��������ǣ�������
��ͼ����ij��ʳƷ��˾�����ǹ���������y��Ԫ����������x��ǧ�ˣ�֮��ĺ���ͼ��������=�����۶�-�ܳɱ������ù�˾��ͨ�������ı��ܳɱ�������ǹ��ۼۡ��ķ���������۲��ѵ���״������������ĸ�ͼ�����߾���ʾ�µ����۷�������������������֮��ĺ���ͼ�����ܷ�ӳ�ù�˾�Ľ��������ǣ�������| A�� | 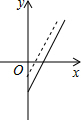 | B�� | 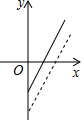 | C�� | 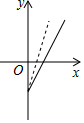 | D�� | 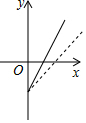 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
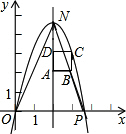 ��ͼ����ֱ������ϵ�У���P�������ǣ�n��0����n��0����������y=-x2+bx+c����ԭ��O�͵�P����֪������ABCD����������ΪA��2��2����B��3��2����D��2��3����
��ͼ����ֱ������ϵ�У���P�������ǣ�n��0����n��0����������y=-x2+bx+c����ԭ��O�͵�P����֪������ABCD����������ΪA��2��2����B��3��2����D��2��3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com