
【题目】如图平行四边形ABCD中,∠ABD=30°,AB=4,AE⊥BD,CF⊥BD,且,E,F恰好是BD的三等分点,又M、N分别是AB,CD的中点,那么四边形MENF的面积是 . 
科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 两条对角线互相平分的四边形是平行四边形
B. 两条对角线相等的四边形是矩形
C. 两条对角线互相垂直的四边形是菱形
D. 两条对角线互相垂直且平分的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图梯形ABCD中,AD∥BC,∠ABC+∠C=90°,AB=6,CD=8,M,N,P分别为AD、BC、BD的中点,则MN的长为( ) 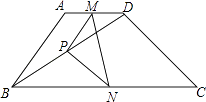
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠A=55°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( ) 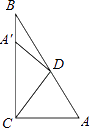
A.40°
B.30°
C.20°
D.10°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景: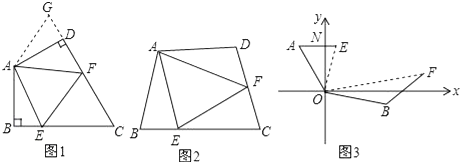
(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF= ![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进.1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅在架设电线时,为了检验三条电线是否互相平行只检查了其中两条是否与第三条平行即可,这样做的道理是______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】((2016江苏省苏州市中考预测)囧(读jiǒng)原是一个今已罕用的文字,由于囧字外观貌似失意的表情,近年在网络间成为一个流行的表情符号.如图是一个近似“囧”的图形,若已知四边形ABCD是一个边长为2a的正方形,P、M、N分别是边AD、AB、CD的中点,E、H分别是PM、PN的中点,则正方形EFGH的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com