
����Ŀ�����ⱳ����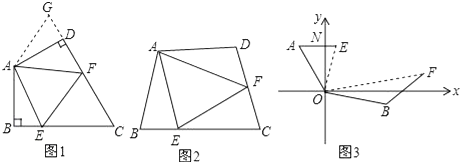
��1����ͼ1�����ı���ABCD�У�AB=AD����BAD=120�㣬��B=��ADC=90�㣮E��F�ֱ���BC��CD�ϵĵ㣮�ҡ�EAF=60�㣮̽��ͼ���߶�BE��EF��FD֮���������ϵ��
С��ͬѧ̽��������ķ����ǣ��ӳ�FD����G��ʹDG=BE������AG����֤����ABE�ա�ADG����֤����AEF�ա�AGF���ɵó����ۣ����Ľ���Ӧ����
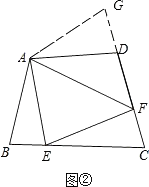
��2����ͼ2�������ı���ABCD�У�AB=AD����B+��D=180�㣮E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF= ![]() ��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
��3����ͼ3����ij�ξ�����ϰ�У���ͧ����ָ�����ģ�O������ƫ��30���A������ͧ����ָ��������ƫ��70���B������������ͧ��ָ�����ĵľ�����ȣ��ӵ��ж�ָ���ͧ��������������60����/Сʱ���ٶ�ǰ������ͧ���ر�ƫ��50��ķ�����80����/Сʱ���ٶ�ǰ��.1.5Сʱ��ָ�����Ĺ۲�ס�������ͧ�ֱ�E��F����������֮ͧ��ļн�Ϊ70�㣬�����ʱ����֮ͧ��ľ��룮
���𰸡�
��1��EF=BE+DF
��2��
�⣺����EF=BE+DF��Ȼ������
���ɣ��ӳ�FD����G��ʹDG=BE������AG����ͼ�ڣ�
�ڡ�ABE�͡�ADG�У� 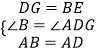
���ABE�ա�ADG��SAS����
��AE=AG����BAE=��DAG��
�ߡ�EAF= ![]() ��BAD��
��BAD��
���GAF=��DAG+��DAF=��BAE+��DAF=��BAD����EAF=��EAF��
���EAF=��GAF��
�ڡ�AEF�͡�GAF�У� 
���AEF�ա�AGF��SAS����
��EF=FG��
��FG=DG+DF=BE+DF��
��EF=BE+DF
��3��
�⣺��ͼ3��
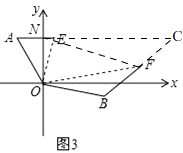
����EF���ӳ�AE��BF�ཻ�ڵ�C��
�ߡ�AOB=30��+90��+��90�㩁70�㣩=140�㣬��EOF=70�㣬
���EOF= ![]() ��AOB��
��AOB��
�֡�OA=OB����OAC+��OBC=��90�㩁30�㣩+��70��+50�㣩=180�㣬
�����̽�������е�������
�����EF=AE+BF������
��EF=1.5����60+80��=210���
�𣺴�ʱ����֮ͧ��ľ�����210����
���������⣺��1��EF=BE+DF��֤�����£�
�ڡ�ABE�͡�ADG�У� 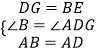
���ABE�ա�ADG��SAS����
��AE=AG����BAE=��DAG��
�ߡ�EAF= ![]() ��BAD��
��BAD��
���GAF=��DAG+��DAF=��BAE+��DAF=��BAD����EAF=��EAF��
���EAF=��GAF��
�ڡ�AEF�͡�GAF�У� 
���AEF�ա�AGF��SAS����
��EF=FG��
��FG=DG+DF=BE+DF��
��EF=BE+DF��
���Դ��� EF=BE+DF��
�����㾫����ͨ��������������ε���������������߹�ϵ�����������ε����=1/2���ס��ߣ�����������֮�ʹ��ڵ����ߣ�����������֮��С�ڵ����ߣ������϶����������߶Σ�������������ε��������Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������κ������ȱ������ε�λ����ͼ��ʾ������3=50�㣬���1+��2=�� �� 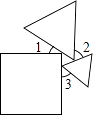
A.90��
B.100��
C.130��
D.180��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����cΪ����������c��0�����в���ʽ����ȷ���ǣ� ��
A.3c��2c
B.![]()
C.3+c��2+c
D.��3c����2c
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼƽ���ı���ABCD�У���ABD=30�㣬AB=4��AE��BD��CF��BD���ң�E��Fǡ����BD�����ȷֵ㣬��M��N�ֱ���AB��CD���е㣬��ô�ı���MENF������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�У���B=90�㣬��AB�ϵ�һ��OΪԲ�ģ���OAΪ�뾶��Բ��AC�ڵ�D����AB�ڵ�E��
��1����֤��ACAD=ABAE��
��2�����BD����O�����ߣ�D���е㣬E��OB���е㣬��BC=2ʱ����AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�IJ���ʽ3x��m��5�Ľ⼯��ͼ��ʾ����m��ֵ���ڣ� ��![]()
A.![]()
B.��1
C.��5
D.��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУѧ����ƹ������ë������������������������˶���Ŀ��ϲ�������ÿλͬѧ������ֻ�ܴ���ѡ��һ������ѡȡ��������ѧ�����г������飬�������������Ƴ��˲�������ͳ��ͼ��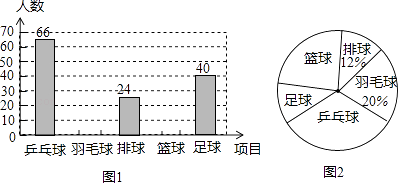
��1���μӵ����ѧ��һ��������ͼ2��ƹ�����������ε�Բ�Ľ�Ϊ�㣻
��2����ͼ1�в�ȫ����ͳ��ͼ��������Ӧ���ݣ���
��3������У����2000��ͬѧ������ݳ����������ݹ��Ƹ�Уͬѧ��ϲ�������˶���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���۲��A�����DE�ĵ�D��ij¥��CB�ĵ�C������һ��ֱ���ϣ��ӵ�A�����¥����B������Ϊ22�㣬��ʱ��Eǡ����AB�ϣ��ӵ�D�����¥����B������Ϊ38.5�㣮��֪���DE�ĸ߶�Ϊ12�ף�����¥��CB�ĸ߶ȣ����ο����ݣ�sin22���0.37��cos22���0.93��tan22���0.40��sin38.5���0.62��cos38.5���0.78��tan38.5���0.80��
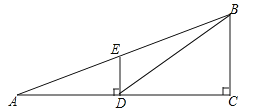
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com