
【题目】如图,观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上,从点A处测得楼顶端B的仰角为22°,此时点E恰好在AB上,从点D处测得楼顶端B的仰角为38.5°.已知旗杆DE的高度为12米,试求楼房CB的高度.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)
科目:初中数学 来源: 题型:
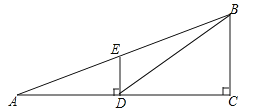
【题目】问题背景:
(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF= ![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进.1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E离开点A后,运动秒时,△DEB与△BCA全等. 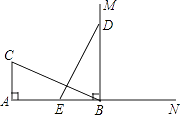
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场销售A、B两种商品,它们的进价和售价如表所示.
A商品 | B商品 | |
进价(元/件) | 30 | 40 |
售价(元/件) | 50 | 70 |
(1)若该商场购进A、B两种商品共60件,恰好用去2050元,求购进A、B两种商品各多少件?
(2)该商场第二次购买A、B两种商品,而B商品数量比A商品数量的2倍少6件,且购买总额不超过2840元,总利润不少于1900元.请你帮助该商场设计相应的进货方案;
(3)若一个星期该商场销售A、B两种商品的总利润恰好是140元,求销售A、B两种商品各多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
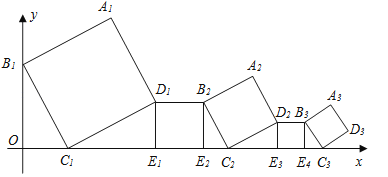
【题目】在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是BC边上的高,AM是△ABC外角∠CAE的平分线. 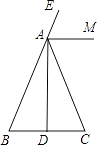
(1)用尺规作图方法,作∠ADC的平分线DN;(保留作图痕迹,不写作法和证明)
(2)设DN与AM交于点F,判断△ADF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.(![]() 取1.73)
取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com