
����Ŀ���̳�����A��B������Ʒ�����ǵĽ��ۺ��ۼ������ʾ��
A��Ʒ | B��Ʒ | |
���ۣ�Ԫ/���� | 30 | 40 |
�ۼۣ�Ԫ/���� | 50 | 70 |
��1�������̳�����A��B������Ʒ��60����ǡ����ȥ2050Ԫ����A��B������Ʒ�����ټ���
��2�����̳��ڶ��ι���A��B������Ʒ����B��Ʒ������A��Ʒ������2����6�����ҹ����ܶ����2840Ԫ������������1900Ԫ������������̳������Ӧ�Ľ���������
��3����һ�����ڸ��̳�����A��B������Ʒ��������ǡ����140Ԫ��������A��B������Ʒ�����ټ���
���𰸡�
��1���⣺����̳�����A����Ʒx����B����Ʒy����������ã�
![]() ��
��
��� ![]() ��
��
�𣺸��̳�����A����Ʒ35����B����Ʒ25����
��2���⣺����̳�����A����Ʒa������B����Ʒ��2a��6��������������ã�
![]() ��
��
���26��a�� ![]() ��
��
��a����������
��a=26��27��28��
���Խ������������֣�
����һ������A����Ʒ26��������B����Ʒ46��
������������A����Ʒ27��������B����Ʒ48��
������������A����Ʒ28��������B����Ʒ50��
��3���⣺����̳�����A����Ʒb��������B����Ʒc������������ɵã�20b+30c=140��
��������
2b+3c=14
bֻ��ȡ1��4��
����A����Ʒ1����B����Ʒ4��������A����Ʒ4����B����Ʒ2����
����������1���ɡ�A��B������Ʒ��60������x+y=60���ɡ�ǡ����ȥ2050Ԫ���ɵ�30x+40y=2050���ⷽ���鼴�ɣ���2�����A����Ʒa�����ɡ�B��Ʒ������A��Ʒ������2����6�����ҹ����ܶ����2840Ԫ���ɵò���ʽ30a+40(2a6)��2860���ɡ�����������1900Ԫ���ɵò���ʽ20a+30(2a6)��1900���ⲻ��ʽ�飬�ҳ������⣬���������⣬���м��ַ�������3���ɡ�������ǡ����140�����ж�Ԫһ�η���20b+30c=140����������⼴��.
�����㾫����������Ҫ������һԪһ�β���ʽ���Ӧ�õ����֪ʶ�㣬��Ҫ����1���������⣬�ҳ����ȹ�ϵ��2���裺��δ֪����3���У��г�����ʽ�飻4���⣺�ⲻ��ʽ�飻5�����飺�Ӳ���ʽ��Ľ⼯���ҳ���������Ĵ𰸣�6����д������𰸲�����ȷ�����⣮


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����cΪ����������c��0�����в���ʽ����ȷ���ǣ� ��
A.3c��2c
B.![]()
C.3+c��2+c
D.��3c����2c
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУѧ����ƹ������ë������������������������˶���Ŀ��ϲ�������ÿλͬѧ������ֻ�ܴ���ѡ��һ������ѡȡ��������ѧ�����г������飬�������������Ƴ��˲�������ͳ��ͼ��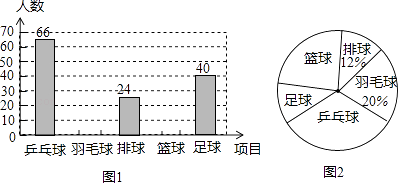
��1���μӵ����ѧ��һ��������ͼ2��ƹ�����������ε�Բ�Ľ�Ϊ�㣻
��2����ͼ1�в�ȫ����ͳ��ͼ��������Ӧ���ݣ���
��3������У����2000��ͬѧ������ݳ����������ݹ��Ƹ�Уͬѧ��ϲ�������˶���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���
��1����ͼ��MN��EF��GH��EF����CAB=90�㣬��1=70�㣬��ABF�Ķ�����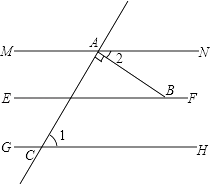
��2�����㣺 ![]() +
+ ![]() +|
+| ![]() ��2|��2��
��2|��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ��ⲻ��ʽ��x+2����x��3����0�������������ij˷�����������ˣ�ͬ�ŵ�����������ת��Ϊ����ʽ����⣮
�⣺��x+2����x��3����0��ת��Ϊ�� ![]() ���
��� ![]() ���ⲻ��ʽ��٣���x��3���ⲻ��ʽ��ڣ���x����2��
���ⲻ��ʽ��٣���x��3���ⲻ��ʽ��ڣ���x����2��
��ԭ����ʽ��x+2����x��3����0�Ľ⼯��x��3��x����2��
�����������ķ����������в���ʽ
��1����x+7����2x+8����0
��2����3x��9����x+11����0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
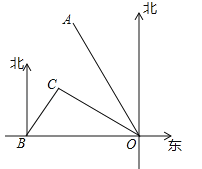
����Ŀ����ͼ��ʾ���ۿ�Bλ�ڸۿ�O��������120km����С��Cλ�ڸۿ�O��ƫ��60��ķ���һ���δ��Ӹۿ�O��������OA����ƫ��30�㣩��vkm/h���ٶ�ʻ��ۿ�O��ͬʱһ�ҿ�ͧ�Ӹۿ�B�������ر�ƫ��30��ķ�����60km/h���ٶ�ʻ��С��C����С��C��1h��װ�������ʺ�������ԭ�����ٶȸ��δ���ȥ��
��1����ͧ�Ӹۿ�B��С��C��Ҫ�ʱ�䣿
��2������ͧ��С��C�����δ�����ǡ����ʱ1h����v��ֵ����������ۿ�O�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
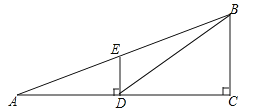
����Ŀ����ͼ���۲��A�����DE�ĵ�D��ij¥��CB�ĵ�C������һ��ֱ���ϣ��ӵ�A�����¥����B������Ϊ22�㣬��ʱ��Eǡ����AB�ϣ��ӵ�D�����¥����B������Ϊ38.5�㣮��֪���DE�ĸ߶�Ϊ12�ף�����¥��CB�ĸ߶ȣ����ο����ݣ�sin22���0.37��cos22���0.93��tan22���0.40��sin38.5���0.62��cos38.5���0.78��tan38.5���0.80��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������1��2��8��5��3��9��5��4��5��4��������_________����λ����__________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com