
【题目】如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E离开点A后,运动秒时,△DEB与△BCA全等. 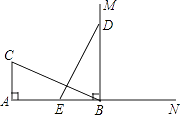
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】为了解某校学生对乒乓球、羽毛球、排球、篮球和足球五种球类运动项目的喜爱情况(每位同学必须且只能从中选择一项),随机选取了若干名学生进行抽样调查,并将调查结果绘制成了不完整的统计图.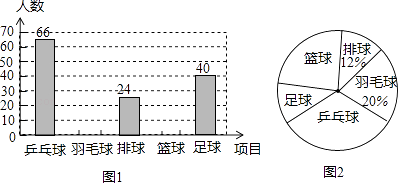
(1)参加调查的学生一共有名,图2中乒乓球所在扇形的圆心角为°;
(2)在图1中补全条形统计图(标上相应数据);
(3)若该校共有2000名同学,请根据抽样调查数据估计该校同学中喜欢足球运动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
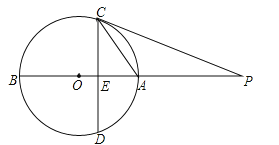
【题目】如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且![]() =PEPO.
=PEPO.
(1)求证:PC是⊙O的切线.
(2)若OE:EA=1:2,PA=6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:解不等式(x+2)(x﹣3)>0,根据有理数的乘法法则“两数相乘,同号得正”,可以转化为不等式组求解.
解:(x+2)(x﹣3)>0,转化为① ![]() 或②
或② ![]() ,解不等式组①,得x>3,解不等式组②,得x<﹣2.
,解不等式组①,得x>3,解不等式组②,得x<﹣2.
∴原不等式(x+2)(x﹣3)>0的解集是x>3或x<﹣2.
请你仿照上面的方法,解下列不等式
(1)(x+7)(2x+8)>0
(2)(3x﹣9)(x+11)<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
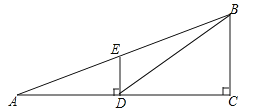
【题目】如图,观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上,从点A处测得楼顶端B的仰角为22°,此时点E恰好在AB上,从点D处测得楼顶端B的仰角为38.5°.已知旗杆DE的高度为12米,试求楼房CB的高度.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学思考: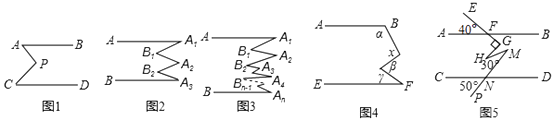
(1)如图1,已知AB∥CD,探究下面图形中∠APC和∠PAB、∠PCD的关系,并证明你的结论
(2)①如图2,已知AA1∥BA1 , 请你猜想∠A1 , ∠B1 , ∠B2 , ∠A2、∠A3的关系,并证明你的猜想;
②如图3,已知AA1∥BAn , 直接写出∠A1 , ∠B1 , ∠B2 , ∠A2、…∠Bn﹣1、∠An的关系
(3)①如图4所示,若AB∥EF,用含α,β,γ的式子表示x,应为
A.180°+α+β﹣γ B.180°﹣α﹣γ+β C.β+γ﹣α D.α+β+γ
②如图5,AB∥CD,且∠AFE=40°,∠FGH=90°,∠HMN=30°,∠CNP=50°,请你根据上述结论直接写出∠GHM的度数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com