
【题目】数学思考: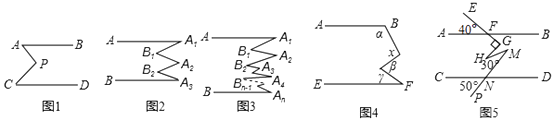
(1)如图1,已知AB∥CD,探究下面图形中∠APC和∠PAB、∠PCD的关系,并证明你的结论
(2)①如图2,已知AA1∥BA1 , 请你猜想∠A1 , ∠B1 , ∠B2 , ∠A2、∠A3的关系,并证明你的猜想;
②如图3,已知AA1∥BAn , 直接写出∠A1 , ∠B1 , ∠B2 , ∠A2、…∠Bn﹣1、∠An的关系
(3)①如图4所示,若AB∥EF,用含α,β,γ的式子表示x,应为
A.180°+α+β﹣γ B.180°﹣α﹣γ+β C.β+γ﹣α D.α+β+γ
②如图5,AB∥CD,且∠AFE=40°,∠FGH=90°,∠HMN=30°,∠CNP=50°,请你根据上述结论直接写出∠GHM的度数是 .
【答案】
(1)证明:如图1,过点P作OP∥AB,
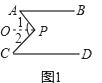
∵AB∥CD,
∴OP∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∴∠APC=∠1+∠2=∠PAB+∠PCD,
即∠APC=∠PAB+∠PCD
(2)解:①如图2,过点A2作A2O∥AA1,
由(1)可知∠B1=∠A1+∠1,∠B2=∠2+∠A3,
所以,∠B1+∠B2=∠A1+∠A2+∠A3;
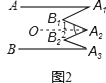
②如图3,由①可知:
∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn﹣1
(3)B,30°
【解析】解:(1)如图1,过点P作OP∥AB,
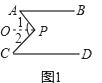
∵AB∥CD,
∴OP∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∴∠APC=∠1+∠2=∠PAB+∠PCD,
即∠APC=∠PAB+∠PCD
(2)①如图2,过点A2作A2O∥AA1,
由(1)可知∠B1=∠A1+∠1,∠B2=∠2+∠A3,
所以,∠B1+∠B2=∠A1+∠A2+∠A3;

②如图3,由①可知:
∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn﹣1
(3)①如图4,过∠x的顶点作CD∥AB,
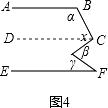
则∠x=(180°﹣α)+(β﹣γ)=180°﹣α﹣γ+β,
②如图5,由(1)可知,40°+∠GHM+50°=∠G+∠M,
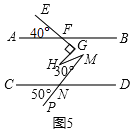
∵∠G=90°,∠M=30°,
∴∠GHM=90°+30°﹣40°﹣50°=30°.
所以答案是:(1)∠APC=∠PAB+∠PCD;(2)∠B1+∠B2=∠A1+∠A2+∠A3;∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn﹣1;(3)B;30°.
【考点精析】通过灵活运用平行线的性质,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补即可以解答此题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E离开点A后,运动秒时,△DEB与△BCA全等. 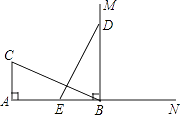
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是BC边上的高,AM是△ABC外角∠CAE的平分线. 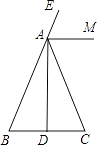
(1)用尺规作图方法,作∠ADC的平分线DN;(保留作图痕迹,不写作法和证明)
(2)设DN与AM交于点F,判断△ADF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A.四个角相等的四边形是矩形
B.对角线相等的平行四边形是矩形
C.对角线垂直的四边形是菱形
D.对角线垂直的平行四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
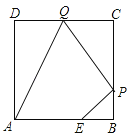
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明命题“三角形中至少有一个内角小于或等于60°”时,首先应该假设这个三角形中( ).
A. 每一个内角都大于60° B. 每一个内角都小于60°
C. 有一个内角大于60° D. 有一个内角小于60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.(![]() 取1.73)
取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com