练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

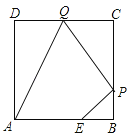
    【题目】如图，已知正方形ABCD边长为3，点E在AB边上且BE=1，点P，Q分别是边BC，CD的动点（均不与顶点重合），当四边形AEPQ的周长取最小值时，四边形AEPQ的面积是 ．

    【答案】．

    【解析】

    试题分析：如图1所示，作E关于BC的对称点E′，点A关于DC的对称点A′，连接A′E′，四边形AEPQ的周长最小，∵AD=A′D=3，BE=BE′=1，∴AA′=6，AE′=4．∵DQ∥AE′，D是AA′的中点，∴DQ是△AA′E′的中位线，∴DQ=AE′=2；CQ=DC﹣CQ=3﹣2=1，∵BP∥AA′，∴△BE′P∽△AE′A′，∴，即，BP=，CP=BC﹣BP==，S四边形AEPQ=S正方形ABCD﹣S△ADQ﹣S△PCQ﹣SBEP=9﹣ADDQ﹣CQCP﹣BEBP=9﹣×3×2﹣×1×﹣×1×=，故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】综合题
    （1）如图，MN∥EF，GH∥EF，∠CAB=90°，∠1=70°，求：∠ABF的度数．

    （2）计算： + +| ﹣2|﹣2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解不等式组，并把解集在数轴上表示出来
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“平行四边形的对角线互相平行”是________事件．（填“必然”、“随机”、“不可能”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学思考：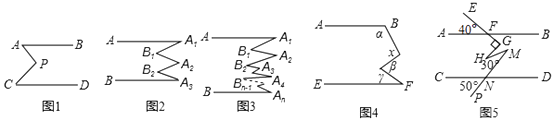

    （1）如图1，已知AB∥CD，探究下面图形中∠APC和∠PAB、∠PCD的关系，并证明你的结论
    （2）①如图2，已知AA1∥BA1 ， 请你猜想∠A1 ， ∠B1 ， ∠B2 ， ∠A2、∠A3的关系，并证明你的猜想；
    ②如图3，已知AA1∥BAn ， 直接写出∠A1 ， ∠B1 ， ∠B2 ， ∠A2、…∠Bn﹣1、∠An的关系
    （3）①如图4所示，若AB∥EF，用含α，β，γ的式子表示x，应为
    A.180°+α+β﹣γ B.180°﹣α﹣γ+β C．β+γ﹣α D．α+β+γ
    ②如图5，AB∥CD，且∠AFE=40°，∠FGH=90°，∠HMN=30°，∠CNP=50°，请你根据上述结论直接写出∠GHM的度数是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列方程是一元二次方程的有（ ）

    A. x（2x+1）=2x（x﹣3）﹣2 B. x2+y=3 C. ax2+bx+c=0 D. x2=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数据1，2，8，5，3，9，5，4，5，4的众数是_________，中位数是__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

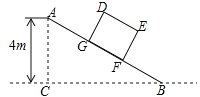
    【题目】如图，某仓储中心有一斜坡AB，其坡度为i=1：2，顶部A处的高AC为4m，B．C在同一水平地面上．

    （1）求斜坡AB的水平宽度BC；

    （2）矩形DEFG为长方体货柜的侧面图，其中DE=2.5m，EF=2m，将该货柜沿斜坡向上运送，当BF=3.5m时，求点D离地面的高．（≈2.236，结果精确到0.1m）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

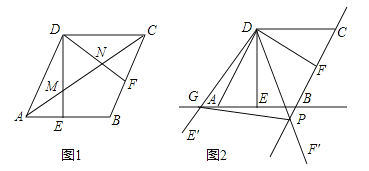
    【题目】如图，在菱形ABCD中，AB=2，∠BAD=60°，过点D作DE⊥AB于点E，DF⊥BC于点F．

    （1）如图1，连接AC分别交DE、DF于点M、N，求证：MN=AC；

    （2）如图2，将△EDF以点D为旋转中心旋转，其两边DE′、DF′分别与直线AB、BC相交于点G、P，连接GP，当△DGP的面积等于时，求旋转角的大小并指明旋转方向．

    查看答案和解析>>

    同步练习册答案