
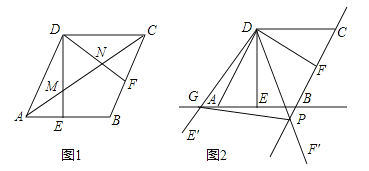
【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.
(1)如图1,连接AC分别交DE、DF于点M、N,求证:MN=![]() AC;
AC;
(2)如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于![]() 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.
【答案】(1)证明见解析;(2)将△EDF以点D为旋转中心,顺时针或逆时针旋转60°.
【解析】
试题分析:(1)连接BD,证明△ABD为等边三角形,根据等腰三角形的三线合一得到AE=EB,根据相似三角形的性质解答即可;
(2)分∠EDF顺时针旋转和逆时针旋转两种情况,根据旋转变换的性质解答即可.
试题解析:(1)证明:如图1,连接BD,交AC于O,在菱形ABCD中,∠BAD=60°,AD=AB,∴△ABD为等边三角形,∵DE⊥AB,∴AE=EB,∵AB∥DC,∴![]() =
=![]() ,同理,
,同理,![]() =
=![]() ,∴MN=
,∴MN=![]() AC;
AC;
(2)解:∵AB∥DC,∠BAD=60°,∴∠ADC=120°,又∠ADE=∠CDF=30°,∴∠EDF=60°,当∠EDF顺时针旋转时,由旋转的性质可知,∠EDG=∠FDP,∠GDP=∠EDF=60°,DE=DF=![]() ,∠DEG=∠DFP=90°,在△DEG和△DFP中,∵∠GDE=∠PDF,∠DEG=∠DFP,DE=DF,∴△DEG≌△DFP,∴DG=DP,∴△DGP为等边三角形,∴△DGP的面积=
,∠DEG=∠DFP=90°,在△DEG和△DFP中,∵∠GDE=∠PDF,∠DEG=∠DFP,DE=DF,∴△DEG≌△DFP,∴DG=DP,∴△DGP为等边三角形,∴△DGP的面积=![]() =
=![]() ,解得,DG=
,解得,DG=![]() ,则cos∠EDG=
,则cos∠EDG=![]() ,∴∠EDG=60°,∴当顺时针旋转60°时,△DGP的面积等于
,∴∠EDG=60°,∴当顺时针旋转60°时,△DGP的面积等于![]() ;
;
同理可得,当逆时针旋转60°时,△DGP的面积也等于![]() ,综上所述,将△EDF以点D为旋转中心,顺时针或逆时针旋转60°时,△DGP的面积等于
,综上所述,将△EDF以点D为旋转中心,顺时针或逆时针旋转60°时,△DGP的面积等于![]() .
.



科目:初中数学 来源: 题型:
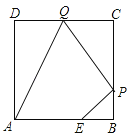
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
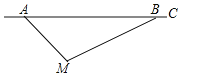
【题目】根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为![]() 米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
(1)求测速点M到该公路的距离;
(2)通过计算判断此车是否超速.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
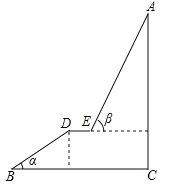
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为[x].即当n为非负整数时,若n﹣ ![]() ≤x<n+
≤x<n+ ![]() ,则[x]=n.如:[3.4]=3,[3.5]=4,…根据以上材料,解决下列问题:
,则[x]=n.如:[3.4]=3,[3.5]=4,…根据以上材料,解决下列问题:
(1)填空:
①若[x]=3,则x应满足的条件:;
②若[3x+1]=3,则x应满足的条件:;
(2)求满足[x]= ![]() x﹣1的所有非负实数x的值.
x﹣1的所有非负实数x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=![]() ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com