
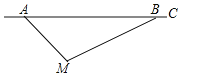
【题目】根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为![]() 米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
(1)求测速点M到该公路的距离;
(2)通过计算判断此车是否超速.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
【答案】(1)10米;(2)此车没有超速.
【解析】
试题分析:(1)过M作MN⊥AB,在Rt△AMN中,由AM=![]() ,∠MAN=45°,sin∠MAN=
,∠MAN=45°,sin∠MAN=![]() 即可求出MN的长,从而的得到结论;
即可求出MN的长,从而的得到结论;
(2)由△AMN为等腰直角三角形得到AN=MN=10米,在Rt△BMN中,求出BN的长,由AN+NB求出AB的长,再求出速度,即可做出判断.
试题解析:(1)过M作MN⊥AB,在Rt△AMN中,AM=![]() ,∠MAN=45°,∴sin∠MAN=
,∠MAN=45°,∴sin∠MAN=![]() ,即
,即![]() ,解得:MN=10,则测速点M到该公路的距离为10米;
,解得:MN=10,则测速点M到该公路的距离为10米;
(2)由(1)知:AN=MN=10米,在Rt△MNB中,∠MBN=30°,由tan∠MBN=![]() ,得:
,得:![]() ,解得:BN=
,解得:BN=![]() (米),∴AB=AN+NB=
(米),∴AB=AN+NB=![]() ≈27.3(米),∴汽车从A到B的平均速度为27.3÷3=9.1(米/秒),∵9.1米/秒=32.76千米/时<40千米/时,∴此车没有超速.
≈27.3(米),∴汽车从A到B的平均速度为27.3÷3=9.1(米/秒),∵9.1米/秒=32.76千米/时<40千米/时,∴此车没有超速.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
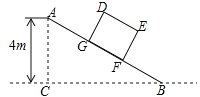
【题目】如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B.C在同一水平地面上.
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(![]() ≈2.236,结果精确到0.1m)
≈2.236,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连结BE、CF.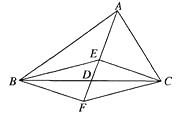
(1)图中的四边形BFCE是平行四边形吗?为什么?
(2)若AB=AC,其它条件不变,那么四边形BFCE是菱形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)已知a+b=-3,ab=5,求多项式4a2b+4ab2-4a-4b的值;
(2)已知x2-3x-1=0,求代数式3-3 x2+9x的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
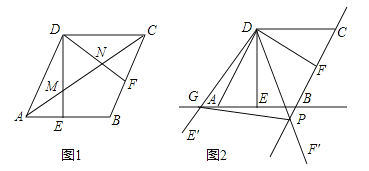
【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.
(1)如图1,连接AC分别交DE、DF于点M、N,求证:MN=![]() AC;
AC;
(2)如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于![]() 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】震惊世界的MH370失联事件发生后第30天,中国“海巡01”轮在南印度洋海域搜索过程中,首次侦听到疑是飞机黑匣子的脉冲信号,探测到的信号所在海域水深4500米左右,其中4500用科学记数法表示为( )
A.4.5×102
B.4.5×103
C.45.0×102
D.0.45×104
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com