
【题目】如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连结BE、CF.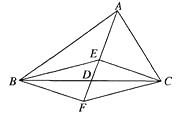
(1)图中的四边形BFCE是平行四边形吗?为什么?
(2)若AB=AC,其它条件不变,那么四边形BFCE是菱形吗?为什么?
【答案】
(1)
是。理由如下:∵在△ABC中,D是BC边的中点,
∴BD=CD,
∵CF∥BE,
∴∠CFD=∠BED,
在△CFD和△BED中,
|
∴△CFD≌△BED(AAS),
∴CF=BE,
∴四边形BFCE是平行四边形.
;
;
;
;
;
;
(2)
是。理由如下:
∵AB=AC,D是BC边的中点,
∴AD⊥BC,
∴EF⊥BC,
∴四边形BECF是菱形.
【解析】(1)证明△CFD≌△BED,再根据平行四边形的判定定理可证得;
(2)由AB=AC,可知△ABC是等腰三角形,根据“三线合一”可得四边形BECF的对角线互相垂直,即可证得.
【考点精析】利用平行四边形的判定和菱形的判定方法对题目进行判断即可得到答案,需要熟知两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是BC边上的高,AM是△ABC外角∠CAE的平分线. 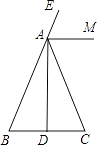
(1)用尺规作图方法,作∠ADC的平分线DN;(保留作图痕迹,不写作法和证明)
(2)设DN与AM交于点F,判断△ADF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明命题“三角形中至少有一个内角小于或等于60°”时,首先应该假设这个三角形中( ).
A. 每一个内角都大于60° B. 每一个内角都小于60°
C. 有一个内角大于60° D. 有一个内角小于60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.(![]() 取1.73)
取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,我们在2016年1月的日历中标出一个十字星,并计算它的“十字差”(将十字星左右两数,上下两数分别相乘再将所得的积作差,称为该十字星的“十字差”).该十字星的十字差为12×14﹣6×20=48,再选择其它位置的十字星,可以发现“十字差”仍为48. 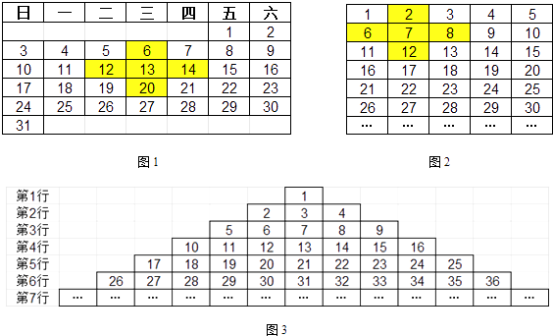
(1)如图2,将正整数依次填入5列的长方形数表中,探究不同位置十字星的“十字差”,可以发现相应的“十字差”也是一个定值,则这个定值为 .
(2)若将正整数依次填入k列的长方形数表中(k≥3),继续前面的探究,可以发现相应“十字差”为与列数k有关的定值,请用k表示出这个定值,并证明你的结论.
(3)如图3,将正整数依次填入三角形的数表中,探究不同十字星的“十字差”,若某个十字星中心的数在第32行,且其相应的“十字差”为2015,则这个十字星中心的数为(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
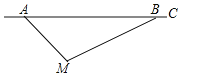
【题目】根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为![]() 米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
(1)求测速点M到该公路的距离;
(2)通过计算判断此车是否超速.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图四边形AOBC为正方形,点C的坐标为(4 ![]() ,0),动点P沿着折线OACB的方向以1个单位每秒的速度匀速运动,同时点Q沿着折线OBCA的方向匀速运动,速度是2个单位长度每秒,运动时间为t秒,当他们相遇时同时停止运动.
,0),动点P沿着折线OACB的方向以1个单位每秒的速度匀速运动,同时点Q沿着折线OBCA的方向匀速运动,速度是2个单位长度每秒,运动时间为t秒,当他们相遇时同时停止运动.
(1)点A的坐标是正方形AOBC的面积是 .
(2)将正方形绕点O顺时针旋转45°,求旋转后的正方形与原正方形的重叠部分的面积.
(3)运动时间t为多少秒时,以A、P、B、Q四点为顶点的四边形为平行四边形?
(4)是否存在这样的t值,使△OPQ成为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com