Question

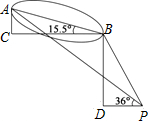
5．有“小蛮腰”之称的广州电视塔为中国第一高电视塔，其主体顶部450～454米处有世界最高摩天轮（即图中AC=4米），与一般竖立的摩天轮不一样，广州塔的摩天轮沿着倾斜的轨道运转，对地倾斜角为∠ABC=15.5°．小明操作无人机观察摩天轮，由于设备限制无法近距离拍摄，无人机在图中P点观察到摩天轮最低点B的仰角为∠BPD=60°，最高点A的仰角为∠APD=36°，请问此时无人机距离电视塔的水平距离PD为（　　）（参考数据：tan15.5°≈0.4，tan36°≈0.7，$\sqrt{3}$≈1.7）

• A． 3
• B． 2.7
• C． 3.3
• D． 3.7

Answer 1

分析 过点延长AC交PD延长线于点E，则AE⊥PE，Rt△ABC中求得DE=BC=$\frac{AC}{tan∠ABC}$≈10、Rt△BDP中得CE=BD=PDtan∠BPD=$\sqrt{3}$PD，根据tan∠APE=$\frac{AE}{PE}$得$\frac{4+\sqrt{3}PD}{10+PD}$≈0.7，解之即可．

解答 解：过点延长AC交PD延长线于点E，
则AE⊥PE，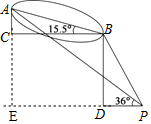

在Rt△ABC中，∵AC=4，∠ABC=15.5°，
∴DE=BC=$\frac{AC}{tan∠ABC}$≈10（m），
在Rt△BDP中，∵∠BPD=60°，
∴CE=BD=PDtan∠BPD=$\sqrt{3}$PD，
在Rt△APE中，∵tan∠APE=$\frac{AE}{PE}$，
∴$\frac{4+\sqrt{3}PD}{10+PD}$≈0.7，
解得：PD≈3，
故选：A．

点评 本题主要考查解直角三角形的应用-仰角俯角问题，熟练掌握三角函数的定义是解题的关键．