
【题目】
九年级数学兴趣小组组织了以“等积变形”为主题的课题研究.
第一学习小组发现:如图(1),点A、点B在直线l1上,点C、点D在直线l2上,若l1∥l2,则S△ABC=S△ABD;反之亦成立.
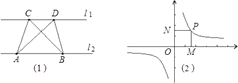
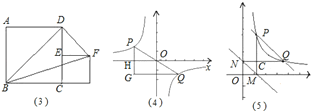
第二学习小组发现:如图(2),点P是反比例函数![]() 上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
请利用上述结论解决下列问题:
(1)如图(3),四边形ABCD、与四边形CEFG都是正方形点E在CD上,正方形ABCD边长为2,则![]() =_________.
=_________.
(2)如图(4),点P、Q在反比例函数![]() 图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若
图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若![]() =8,则
=8,则![]() =_________,k=_________.
=_________,k=_________.
(3)如图(5)点P、Q是第一象限的点,且在反比例函数![]() 图象上,过点P作x轴垂线,过点Q作y轴垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
图象上,过点P作x轴垂线,过点Q作y轴垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
【答案】(1)2;(2)2、-4;(3)PQ∥MN
【解析】
(1)根据组合图形的面积求法得出三角的面积;(2)根据反比例的性质以及三角形的面积的求法进行求法;(3)作PA⊥y轴,QB⊥x轴,垂足为A,B,连接PN,MQ,根据双曲线的性质进行计算.
解:(1)连接CF,
∵四边形ABCD与四边形CEFG都是正方形,
∴CF∥BD,△CBD与△FBD同底等高,
∴S△BDF=S△BDC=![]() S正方形ABCD=2;
S正方形ABCD=2;
故答案为: 2.
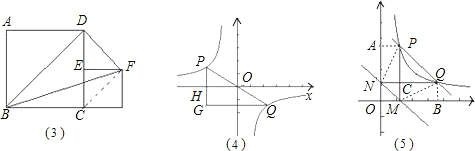
(2)设P(x,y),则k=xy,
根据题意,得GQ=-2x,PG=2y,
∴S△PQG=![]() ×GQ×PG=8,即
×GQ×PG=8,即![]() (-2x)2y=8,
(-2x)2y=8,
解得xy=-4,即k=-4,
S△POH=![]() ×OH×PH=-
×OH×PH=-![]() xy=2;
xy=2;
故答案为: 2,-4.
(3)PQ∥MN.
理由:作PA⊥y轴,QB⊥x轴,垂足为A,B,连接PN,MQ,
根据双曲线的性质可知,S矩形AOMP=S矩形BONQ=k,
∴S矩形ANCP=S矩形BMCQ,可知S△NCP=S△MCQ,
∴S△NPQ=S△MPQ,
∴PQ∥MN.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
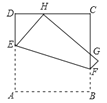
【题目】如图,将正方形ABCD折叠,使点A与CD边上的点H重合(H不与C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD周长为m,△CHG周长为n,则![]() 为( )
为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
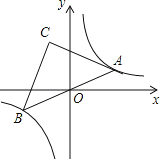
【题目】如图,反比例函数y=![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=![]() 的图象上运动,tan∠CAB=2,则k=_____.
的图象上运动,tan∠CAB=2,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的是①AB的长等于圆内接正六边形的边长 ②弦AC的长等于圆内接正十二边形的边长 ③弧![]() 弧
弧![]() ④∠BAC=30°
④∠BAC=30°
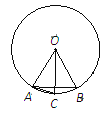
A.①②④B.①③④C.②③④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三辆汽车经过某收费站下高速时,在2个收费通道A,B中,可随机选择其中的一个通过.
(1)三辆汽车经过此收费站时,都选择A通道通过的概率是 ;
(2)求三辆汽车经过此收费站时,至少有两辆汽车选择B通道通过的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=![]() 的图象在第一象限的交点为C,CD⊥x轴于D,若OB=3,OD=6,△AOB的面积为3.
的图象在第一象限的交点为C,CD⊥x轴于D,若OB=3,OD=6,△AOB的面积为3.
(1)求一次函数与反比例函数的表达式;
(2)当x>0时,比较kx+b与![]() 的大小.
的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
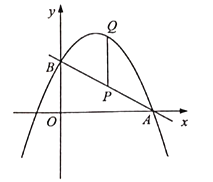
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() (
(![]() ),与
),与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() (
(![]() )经过
)经过![]() ,
,![]() 两点,
两点,![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() .
.
(1)当![]() 时,
时,
①求抛物线的关系式;
②设点![]() 的横坐标为
的横坐标为![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的长,并求当
的长,并求当![]() 为何值时,
为何值时,![]() ?
?
(2)若![]() 长的最大值为16,试讨论关于
长的最大值为16,试讨论关于![]() 的一元二次方程
的一元二次方程![]() 的解的个数与
的解的个数与![]() 的取值范围的关系.
的取值范围的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
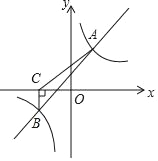
【题目】如图所示,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,4),B(﹣4,n)两点.
的图象交于A(2,4),B(﹣4,n)两点.
(1)分别求出一次函数与反比例函数的表达式;
(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com