
【题目】如图所示,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的是①AB的长等于圆内接正六边形的边长 ②弦AC的长等于圆内接正十二边形的边长 ③弧![]() 弧
弧![]() ④∠BAC=30°
④∠BAC=30°
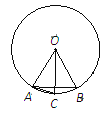
A.①②④B.①③④C.②③④D.①②③
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】某药品生产基地共有5条生产线,每条生产线每月生产药品20万盒,该基地打算从第一个月开始到第五个月结束,对每条生产线进行升级改造.改造时,每个月只升级改造一条生产线,这条生产线当月停产,并于下个月投入生产,其他生产线则正常生产.经调查,每条生产线升级改造后,每月的产量会比原来提高20%.
(1)根据题意,完成下面问题:
①把下表补充完整(直接写在横线上):
月数 | 第1个月 | 第2个月 | 第3个月 | 第4个月 | 第5个月 | 第6个月 | … |
产量/万盒 |
|
|
| 92 | … | … | … |
②从第1个月进行升级改造后,第 个月的产量开始超过未升级改造时的产量;
(2)若该基地第x个月(1≤x≤5,且x是整数)的产量为y万盒,求y关于x的函数关系式;
(3)已知每条生产线的升级改造费是30万元,每盒药品可获利3元.设从第1个月开始升级改造后,生产药品所获总利润为W1万元;同时期内,不升级改造所获总利润为W2万元设至少到第n个月(n为正整数)时,W1大于W2,求n的值.(利润=获利﹣改造费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=4,CD=2,O为AD的中点,以AD为直径的弧DE与BC相切于点E,连接BD,则阴影部分的面积为( )

A.πB.![]() C.π+2D.
C.π+2D.![]() +4
+4
查看答案和解析>>
科目:初中数学 来源: 题型:
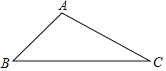
【题目】超速行驶被称为“马路第一杀手”,为了让驾驶员自觉遵守交通规则,市公路检测中在一事故多发地段安装了一个测速仪器,如图所示,已知检测点A设在距离公路BC20米处,∠B=45°,∠C=30°,现测得一辆汽车从B处行驶到C处所用时间为2.7秒.
(1)求B,C之间的距离(结果保留根号);
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:![]() 1.7,
1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
九年级数学兴趣小组组织了以“等积变形”为主题的课题研究.
第一学习小组发现:如图(1),点A、点B在直线l1上,点C、点D在直线l2上,若l1∥l2,则S△ABC=S△ABD;反之亦成立.
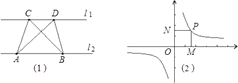
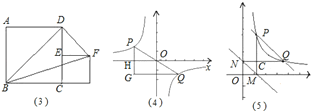
第二学习小组发现:如图(2),点P是反比例函数![]() 上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
请利用上述结论解决下列问题:
(1)如图(3),四边形ABCD、与四边形CEFG都是正方形点E在CD上,正方形ABCD边长为2,则![]() =_________.
=_________.
(2)如图(4),点P、Q在反比例函数![]() 图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若
图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若![]() =8,则
=8,则![]() =_________,k=_________.
=_________,k=_________.
(3)如图(5)点P、Q是第一象限的点,且在反比例函数![]() 图象上,过点P作x轴垂线,过点Q作y轴垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
图象上,过点P作x轴垂线,过点Q作y轴垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,AB=![]() ,tan∠ABC=2,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.
,tan∠ABC=2,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.
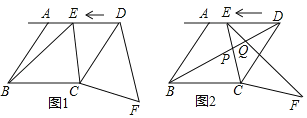
(1)求证:BE=DF;
(2)当t= 秒时,DF的长度有最小值,最小值等于 ;
(3)如图2,连接BD、EF、BD交EC、EF于点P、Q,当t为何值时,△EPQ是直角三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com