
 如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处,若AB=3,AD=4,则ED的长为( )
如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处,若AB=3,AD=4,则ED的长为( )| A. | $\frac{4}{3}$ | B. | 3 | C. | 1 | D. | $\frac{3}{2}$ |
分析 首先利用勾股定理计算出AC的长,再根据折叠可得△DEC≌△D′EC,设ED=x,则D′E=x,AD′=AC-CD′=2,AE=4-x,再根据勾股定理可得方程22+x2=(4-x)2,再解方程即可.
解答 解:∵AB=3,AD=4,
∴DC=3,BC=4
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
根据折叠可得:△DEC≌△D′EC,
∴D′C=DC=3,DE=D′E,
设ED=x,则D′E=x,AD′=AC-CD′=2,AE=4-x,
在Rt△AED′中:(AD′)2+(ED′)2=AE2,
22+x2=(4-x)2,
解得:x=$\frac{3}{2}$.
故选:D.
点评 此题主要考查了图形的翻着变换,以及勾股定理的应用,关键是掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}+\frac{1}{2}=-2$ | B. | $(-\frac{1}{3}{)^2}=\frac{1}{9}$ | C. | |3|=3 | D. | $\sqrt{12}=2\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 571(1+x)=1100 | B. | 571(1+2x)=1100 | ||
| C. | 571(1+x)2=1100 | D. | 571(1+x)+571(1+x)2=1100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
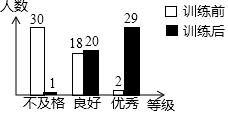 某校九年级700名学生在2016年中考体育考试前对跑步进行了强化训练,在训练前后进行了二次测试,测试成绩都以同一标准(10分为满分)划分成“不及格(7分及以下)”、“良好(9分或8分)”和“优秀(10分)”三个等级.为了了解强化训练的效果,用随机方式抽取了九年级学生中50名学生的前后两次测试成绩的等级,并绘制成如图所示的统计图,试结合图形信息回答下列问题:
某校九年级700名学生在2016年中考体育考试前对跑步进行了强化训练,在训练前后进行了二次测试,测试成绩都以同一标准(10分为满分)划分成“不及格(7分及以下)”、“良好(9分或8分)”和“优秀(10分)”三个等级.为了了解强化训练的效果,用随机方式抽取了九年级学生中50名学生的前后两次测试成绩的等级,并绘制成如图所示的统计图,试结合图形信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>-2 | B. | x≤4 | C. | -2<x≤4 | D. | 无解 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com