
ЁОЬтФПЁПШчЭМ1ЃЌPЮЊЁЯMONЦНЗжЯпOCЩЯвЛЕуЃЌвдPЮЊЖЅЕуЕФЁЯAPBСНБпЗжБ№гыЩфЯпOMКЭONНЛгкAЁЂBСНЕуЃЌШчЙћЁЯAPBдкШЦЕуPа§зЊЪБЪМжеТњзуOAOB=OP2 ЃЌ ЮвУЧОЭАбЁЯAPBНазіЁЯMONЕФЙиСЊНЧЃЎ
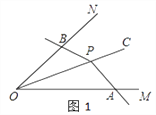
ЃЈ1ЃЉШчЭМ2ЃЌPЮЊЁЯMONЦНЗжЯпOCЩЯвЛЕуЃЌЙ§PзїPBЁЭONгкBЃЌAPЁЭOCгкPЃЌФЧУДЁЯAPB________ЁЯMONЕФЙиСЊНЧЃЈЬюЁАЪЧЁБЛђЁАВЛЪЧЁБЃЉЃЎ
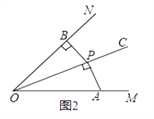
ЃЈ2ЃЉЂйШчЭМ3ЃЌШчЙћЁЯMON=60ЁуЃЌOP=2ЃЌЁЯAPBЪЧЁЯMONЕФЙиСЊНЧЃЌСЌНгABЃЌЧѓЁїAOBЕФУцЛ§КЭЁЯAPBЕФЖШЪ§ЃЛ
ЂкШчЙћЁЯMON=ІСЁуЃЈ0ЁуЃМІСЁуЃМ90ЁуЃЉЃЌOP=mЃЌЁЯAPBЪЧЁЯMONЕФЙиСЊНЧЃЌжБНггУКЌгаІСКЭmЕФДњЪ§ЪНБэЪОЁїAOBЕФУцЛ§ЃЎ
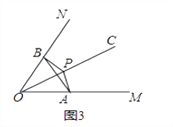
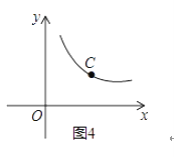
ЃЈ3ЃЉШчЭМ4ЃЌЕуCЪЧКЏЪ§y=![]() ЃЈxЃО0ЃЉЭМЯѓЩЯвЛИіЖЏЕуЃЌЙ§ЕуCЕФжБЯпCDЗжБ№НЛxжсКЭyжсгкAЃЌBСНЕуЃЌЧвТњзуBC=2CAЃЌжБНгаДГіЁЯAOBЕФЙиСЊНЧЁЯAPBЕФЖЅЕуPЕФзјБъЃЎ
ЃЈxЃО0ЃЉЭМЯѓЩЯвЛИіЖЏЕуЃЌЙ§ЕуCЕФжБЯпCDЗжБ№НЛxжсКЭyжсгкAЃЌBСНЕуЃЌЧвТњзуBC=2CAЃЌжБНгаДГіЁЯAOBЕФЙиСЊНЧЁЯAPBЕФЖЅЕуPЕФзјБъЃЎ
ЁОД№АИЁПЪЧ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЯШХаЖЯГіЁїOBPЁзЁїOPAЃЌМДПЩЃЛ
ЃЈ2ЃЉЯШИљОнЙиСЊНЧЧѓГіOAЁСOB=4ЃЌдйРћгУШ§НЧаЮЕФУцЛ§ЙЋЪНЃЌвдМАЯрЫЦЃЌЕУЕНЁЯOAP=ЁЯOPBЃЌМДПЩЃЛ
ЃЈ3ЃЉИљОнЬѕМўЗжЧщПіЬжТлЃЌЕуBдкyжсе§АыжсКЭИКАыжсЃЌдкИКАыжсЪБЃЌОЙ§МЦЫуЃЌВЛДцдкЃЌЂкдке§АыжсЪБЃЌгЩBC=2ACХаЖЯГіЕуCЪЧЯпЖЮABЕФвЛИіШ§ЕШЗжЕуЃЌМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпPЮЊЁЯMONЦНЗжЯпOCЩЯвЛЕуЃЌ
ЁрЁЯBOP=ЁЯAOPЃЌ
ЁпPBЁЭONгкBЃЌAPЁЭOCгкPЃЌ
ЁрЁЯOBP=ЁЯOPAЃЌ
ЁрЁїOBPЁзЁїOPAЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрOP2=OAЁСOBЃЌ
ЁрЁЯAPBЪЧЁЯMONЕФЙиСЊНЧЃЎ
ЙЪД№АИЮЊЪЧЃЎ
ЃЈ2ЃЉЂйШчЭМЃЌЙ§ЕуAзїAHЁЭOBЃЌ
ЁпЁЯAPBЪЧЁЯMONЕФЙиСЊНЧЃЌOP=2ЃЌ
ЁрOAЁСOB=OP2=4ЃЌ
дкRtЁїAOHжаЃЌЁЯAOH=90ЁуЃЌ
ЁрsinЁЯAOH=![]() ЃЌ
ЃЌ
ЁрAH=OAsinЁЯAOHЃЌ
ЁрSЁїAOB=![]() OBЁСAH=
OBЁСAH=![]() OBЁСOAЁСsin60Ёу=
OBЁСOAЁСsin60Ёу=![]() ЁСOP2ЁС
ЁСOP2ЁС![]() =
=![]() ЃЌ
ЃЌ
ЁпOP2=OAЁСOBЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЕуPЮЊЁЯMONЕФЦНЗжЯпЩЯвЛЕуЃЌ
ЁрЁЯAOP=ЁЯBOP=![]() ЁЯMON=30ЁуЃЌ
ЁЯMON=30ЁуЃЌ
ЁрЁїAOPЁзЁїPOBЃЌ
ЁрЁЯOAP=ЁЯOPBЃЌ
ЁрЁЯAPB=ЁЯOPB+ЁЯOPA=ЁЯOAP+ЁЯOPA=180Ёу-30Ёу=150ЁуЃЌ
ЂкгЩЂйгаЃЌSЁїAOB=![]() OBЁСOAЁСЁЯMON=
OBЁСOAЁСЁЯMON=![]() m2ЁСsinІСЃЛ
m2ЁСsinІСЃЛ
ЃЈ3ЃЉЁпЙ§ЕуCЕФжБЯпCDЗжБ№НЛxжсКЭyжсгкAЃЌBСНЕуЃЌЧвТњзуBC=2CAЃЌ
ЁржЛгаЕуAдкxжсе§АыжсЃЌ
ЂйЕБЕуBдкyжсИКАыжсЪБЃЌЕуAжЛФмдкxжсе§АыжсЃЎМДЃКЕуPжЛФмдкЕкЫФЯѓЯоЃЌ
ЩшAЃЈmЃЌ0ЃЉЃЌBЃЈ0ЃЌnЃЉЃЈmЃО0ЃЌnЃМ0ЃЉ
ЁрOA=mЃЌOB=-nЃЌ
ЁпBC=2CAЃЌ
ЁрЕуAЪЧBCжаЕуЃЌ
ЁрЕуCЃЈ2mЃЌ-nЃЉЃЌ
ЁпЕуCдкЫЋЧњЯпy=![]() ЩЯЃЌ
ЩЯЃЌ
Ёр2mЁСЃЈ-nЃЉ=2ЃЌ
Ёрmn=-1ЃЌ
ЁпЁЯAOBЕФЙиСЊНЧЁЯAPB
ЁрOP2=OAЁСOB=|m||n|=1span>ЃЌ
ЁрOP=1ЃЌ
ЁпЕуPдкЁЯAOBЕФЦНЗжЯпЩЯЃЌЩшPЃЈaЃЌ-aЃЉЃЈaЃО0ЃЉЃЌ
ЁрOP2=2a2ЃЌ
Ёр2a2=1ЃЌ
Ёрa=![]() Лђa=-
Лђa=-![]() ЃЈЩсЃЉЃЌ
ЃЈЩсЃЉЃЌ
ЁрЕуPЃЈ![]() ЃЌ-
ЃЌ-![]() ЃЉ
ЃЉ
ЂкЕБЕуBдкyжсе§АыжсЃЌгЩгкBC=2CAЃЌЫљвдЃЌЕуAжЛФмдкxжсе§АыжсЩЯЃЌ
ЩшAЃЈmЃЌ0ЃЉЃЌBЃЈ0ЃЌnЃЉЃЈmЃО0ЃЌnЃО0ЃЉ
ЁрЕуCЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌ
ЃЉЃЌ
Ёр![]() ЁС
ЁС![]() =2ЃЌ
=2ЃЌ
Ёрmn=9ЃЌ
ЁпЁЯAOBЕФЙиСЊНЧЁЯAPB
ЁрOP2=OAЁС0B=mn=9ЃЌ
ЁрOP=3ЃЌ
ЁпЕуPдкЁЯAOBЕФЦНЗжЯпЩЯЃЌМДЃКЕуPдкЕквЛЯѓЯоЃЌЩшPЃЈaЃЌaЃЉЃЌЃЈaЃО0ЃЉ
ЁрOP2=2a2ЃЌ
Ёр2a2=9ЃЌ
Ёрa=![]() Лђa=-
Лђa=-![]() ЃЈЩсЃЉ
ЃЈЩсЃЉ
МДЃКЕуPЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌ
ЃЉЃЌ
злЩЯЫљЪіЃЌЕуPЕФзјБъЮЊЃКЃЈ![]() ЃЌ-
ЃЌ-![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДгЙВЯэЕЅГЕЃЌЙВЯэЦћГЕЕШЙВЯэГіааЕНЙВЯэгъЩЁЕШЙВЯэЮяЦЗЃЌИїЪНИїбљЕФЙВЯэОМУФЃЪНдкИїИіСьгђбИЫйЕФЦеМАЃЎ
(1) ЮЊЛёЕУЖЋЬЈЪаЪаУёВЮгыЙВЯэОМУЕФЛюЖЏаХЯЂЃЌЯТСаЕїВщЗНЪНжаБШНЯКЯРэЕФЪЧЁЁ ЁЁЃЛ
AЃЎЖдФГбЇаЃЕФШЋЬхЭЌбЇНјааЮЪОэЕїВщ
BЃЎЖдФГаЁЧјЕФзЁЛЇНјааЮЪОэЕїВщ
CЃЎдкШЋЪаРяЕФВЛЭЌЩчЧјЃЌбЁШЁВПЗжЪаУёНјааЮЪОэЕїВщ
(2) ЕїВщаЁзщЫцЛњЕїВщСЫЖЋЬЈЪаУёЦяЙВЯэЕЅГЕЧщПіЃЌФГЩчЧјФъСфдк12ЁЋ36ЫъЕФШЫга1000ШЫЃЌДгжаЫцЛњГщШЁСЫ100ШЫЃЌЭГМЦСЫЫћУЧЦяЙВЯэЕЅГЕЕФШЫЪ§ЃЌВЂЛцжЦСЫШчЯТВЛЭъећЕФЭГМЦЭМБэЃЎ
ЦяЙВЯэЕЅГЕЕФШЫЪ§ЭГМЦБэ
ФъСфЖЮ(Ыъ) | ЦЕЪ§ | ЦЕТЪ |
12ЁмxЃМ16 | 2 | 0.02 |
16ЁмxЃМ20 | 3 | 0.03 |
20ЁмxЃМ24 | 15 | a |
24ЁмxЃМ28 | 25 | 0.25 |
28ЁмxЃМ32 | b | 0.30 |
32ЁмxЃМ36 | 25 | 0.25 |
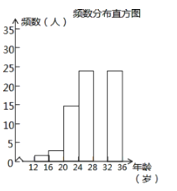
ИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
Ђй ЧѓГіЭГМЦБэжаЕФaЁЂbЃЌВЂВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
Ђк ЪдЙРМЦетИіЩчЧјФъСфдк20ЫъЕН32Ыъ(КЌ20ЫъЃЌВЛКЌ32Ыъ)ЦяЙВЯэЕЅГЕЕФШЫгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЕШЪН![]() дкЪЕЪ§ЗЖЮЇФкГЩСЂЃЌЦфжаaЁЂxЁЂyЪЧСНСНВЛЭЌЕФЪЕЪ§ЃЌдђ
дкЪЕЪ§ЗЖЮЇФкГЩСЂЃЌЦфжаaЁЂxЁЂyЪЧСНСНВЛЭЌЕФЪЕЪ§ЃЌдђ![]() ЕФжЕЪЧ(ЁЁЁЁ)
ЕФжЕЪЧ(ЁЁЁЁ)
A. 3 B. ![]() C. 2 D.
C. 2 D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
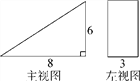
ЁОЬтФПЁПгавЛИіМИКЮЬхЕФаЮзДЮЊжБШ§РтжљЃЌгвЭМЪЧЫќЕФжїЪгЭМКЭзѓЪгЭМЃЎ
(1)ЧыВЙЛГіЫќЕФИЉЪгЭМЃЌВЂБъГіЯрЙиЪ§ОнЃЛ
(2)ИљОнЭМжаЫљБъЕФГпДч(ЕЅЮЛЃКРхУз)ЃЌМЦЫуетИіМИКЮЬхЕФШЋУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy= ![]() x2+bxЉ2гыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкCЕуЃЌЧвAЃЈЉ1ЃЌ0ЃЉЃЎ
x2+bxЉ2гыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкCЕуЃЌЧвAЃЈЉ1ЃЌ0ЃЉЃЎ
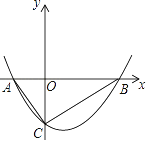
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉХаЖЯЁїABCЕФаЮзДЃЌжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИпаТвЛжааТЭМЪщЙндкЁАаЃдАЪщЯуЫФвчЁБЛюЖЏжагРДСЫНшЪщИпГБЃЌЩЯжмНшЪщМЧТМШчЯТБэЃКЃЈГЌЙ§100ВсЕФВПЗжМЧЮЊе§ЃЌЩйгк100ВсЕФВПЗжМЧЮЊИКЃЉ
ЃЈ1ЃЉЩЯаЧЦкНшЪщзюЖрЕФвЛЬьБШНшЪщзюЩйЕФвЛЬьЖрНшГіЭМЪщЖрЩйВсЃП
ЃЈ2ЃЉЩЯаЧЦкЦНОљУПЬьНшГіЖрЩйВсЪщЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃОХФъМЖОйааБЯвЕЕфРёЃЌашвЊДгОХЃЈ1ЃЉАрЕФ2УћФаЩњ1УћХЎЩњЁЂОХЃЈ2ЃЉЕФ1УћФаЩњ1УћХЎЩњЙВ5ШЫжабЁГі2УћжїГжШЫЃЎ
ЃЈ1ЃЉгУЪїаЮЭМЛђСаБэЗЈСаГіЫљгаПЩФмЧщаЮЃЛ
ЃЈ2ЃЉЧѓ2УћжїГжШЫРДздВЛЭЌАрМЖЕФИХТЪЃЛ
ЃЈ3ЃЉЧѓ2УћжїГжШЫЧЁКУ1Фа1ХЎЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
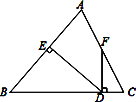
ЁОЬтФПЁПШчЭМЫљЪОЃЌЁїABCжаЃЌAB=BCЃЌDEЁЭABгкЕуEЃЌDFЁЭBCгкЕуDЃЌНЛACгкFЃЎ
ЂХШєЁЯAFD=155ЁуЃЌЧѓЁЯEDFЕФЖШЪ§ЃЛ
ЂЦШєЕуFЪЧACЕФжаЕуЃЌЧѓжЄЃКЁЯCFD=![]() ЁЯBЃЎ
ЁЯBЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЗРвпаТЙкзДВЁЖОЦкМфЃЌЪаУёЖдвНгУПкежЕФашЧѓдНРДдНДѓ.ФГвЉЕъЕквЛДЮгУ2000дЊЙКНјвНгУПкежШєИЩИіЃЌЕкЖўДЮгжгУ2000дЊЙКНјИУПюПкежЃЌЕЋЕкЖўДЮУПИіПкежЕФНјМлЪЧЕквЛДЮНјМлЕФ1.25БЖЃЌЙКНјЕФЪ§СПБШЕквЛДЮЩй200Иі.
ЂХЧѓЕквЛДЮКЭЕкЖўДЮЗжБ№ЙКНјЕФвНгУПкежЪ§СПЮЊЖрЩйИіЃП
ЂЦвЉЕъЕквЛДЮЙКНјПкежКѓЃЌЯШвдУПИі3дЊЕФМлИёГіЪлЃЌТєГіСЫaИіКѓЙКНјЕкЖўХњЭЌПюежЃЌгЩгкНјМлЬсИпСЫЃЌвЉЕъНЋПкежЕФЪлМлвВЬсЩ§жСУПИі3.5дЊМЬајЯњЪлТєГіСЫbИіКѓЃЌСНДЮЙВЪеШы4800дЊ.вђЕБЕивНдКвНСЦЮязЪНєШБЃЌвЉЕъОіЖЈНЋЪЃгрЕФПкежШЋВПОшдљИјвНдК.ЧыЮЪвЉЕъОшдљПкежжСЩйгаЖрЩйИіЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com