
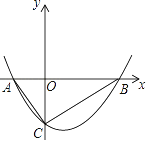
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式;
(2)判断△ABC的形状,证明你的结论.
【答案】(1)y= ![]() x2﹣
x2﹣ ![]() x﹣2;(2)见解析
x﹣2;(2)见解析
【解析】试题分析:(1)因为点A在抛物线上,所以将点A代入函数解析式即可求得;
(2)由函数解析式可以求得其与x轴、y轴的交点坐标,即可求得AB、BC、AC的长,由勾股定理的逆定理可得三角形的形状.
试题解析:(1)∵点A(-1,0)在抛物线y=![]() x2+bx-2上,
x2+bx-2上,
∴![]() ×(-1)2+b×(-1)-2=0,b=-
×(-1)2+b×(-1)-2=0,b=-![]()
∴抛物线的解析式为y=![]() x2-
x2-![]() x-2
x-2
(2)当x=0时y=-2,
∴C(0,-2),OC=2.
当y=0时, ![]() x2-
x2-![]() x-2=0,
x-2=0,
∴x1=-1,x2=4,
∴B(4,0).
∴OA=1,OB=4,AB=5.
∵AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,
∴AC2+BC2=AB2.
∴△ABC是直角三角形.


科目:初中数学 来源: 题型:
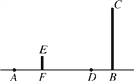
【题目】如图,在一座大厦(图中BC所示)前面30m的地面上,有一盏地灯A照射大厦,身高为1.6m的小亮(图中EF所示)站在大厦和灯之间,若小亮从现在所处位置径直走向大厦,当他走到距离大厦只有5m的D处时停下.
(1)请在图中画出此时小亮的位置(可用线段表示)及他在地灯照射下投在大厦BC上的影子;
(2)请你求出此时小亮的影长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬“雷锋精神”,我县开展“做雷锋精神种子.当四品八德少年”主题征文比赛,已知每篇参赛征文成绩记![]() 分(
分(![]() ) ,组委会从
) ,组委会从![]() 篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如图不完整的两幅统计图表.
篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如图不完整的两幅统计图表.
县主题征文比赛成绩频数分布表
分数段 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
县主题征文比赛成绩频数分布直方图
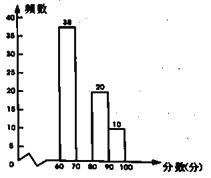
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中![]() 的值是 ;
的值是 ;
(2)补全征文比赛成绩频数分布直方图:
(3)若![]() 分以上(含
分以上(含![]() 分)的征文将被评为一等奖,请估算全县获得一等奖征文的篇数.
分)的征文将被评为一等奖,请估算全县获得一等奖征文的篇数.
查看答案和解析>>
科目:初中数学 来源: 题型:
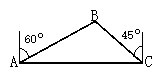
【题目】海船以5海里/小时的速度向正东方向行驶,在A处看见灯塔B在海船的北偏东60°方向,2小时后船行驶到C处,发现此时灯塔B在海船的北偏西45°方向,求此时灯塔B到C处的距离。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P为∠MON平分线OC上一点,以P为顶点的∠APB两边分别与射线OM和ON交于A、B两点,如果∠APB在绕点P旋转时始终满足OAOB=OP2 , 我们就把∠APB叫做∠MON的关联角.
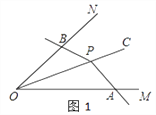
(1)如图2,P为∠MON平分线OC上一点,过P作PB⊥ON于B,AP⊥OC于P,那么∠APB________∠MON的关联角(填“是”或“不是”).
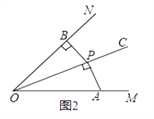
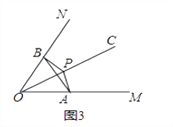
(2)①如图3,如果∠MON=60°,OP=2,∠APB是∠MON的关联角,连接AB,求△AOB的面积和∠APB的度数;
②如果∠MON=α°(0°<α°<90°),OP=m,∠APB是∠MON的关联角,直接用含有α和m的代数式表示△AOB的面积.
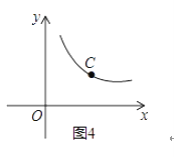
(3)如图4,点C是函数y=![]() (x>0)图象上一个动点,过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,直接写出∠AOB的关联角∠APB的顶点P的坐标.
(x>0)图象上一个动点,过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,直接写出∠AOB的关联角∠APB的顶点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,CD=2![]() .
.
①若∠C=30°,求图中阴影部分的面积;
②若![]() ,求BE的长.
,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com