
【题目】已知二次函数y=2x2﹣4x﹣6.
(1)写出抛物线的开口方向,对称轴和顶点坐标.
(2)在平面直角坐标系中,画出这个二次函数的图象; 
(3)当x取何值时,y随x的增大而减少?
(4)求函数图象与两坐标轴交点所围成的三角形的面积.
【答案】
(1)解:∵a=2>0,
∴抛物线的开口向上,
∵y=2x2﹣4x﹣6=2(x﹣1)2﹣8,
∴抛物线对称轴为直线x=1,
顶点坐标为(1,﹣8)
(2)解:令y=0,2x2﹣4x﹣6=0,
解得x1=﹣1,x2=3,
所以,抛物线与x轴的交点坐标为(﹣1,0),(3,0),
令x=0,则y=﹣6,
所以,抛物线与y轴的交点坐标为(0,﹣6),
作出函数图象如图所示

(3)解:x<1时,y随x的增大而减少
(4)解:函数图象与x轴的交点设为A、B,则AB=3﹣(﹣1)=3+1=4,
设与y轴的交点坐标为(0,﹣6),则OC=6,
所以,函数图象与两坐标轴交点所围成的三角形的面积= ![]() ABOC=
ABOC= ![]() ×4×6=12
×4×6=12
【解析】(1)根据二次项系数大于0判断出开口向上,将二次函数解析式整理成顶点式形式,然后写成对称轴和顶点坐标即可;(2)求出二次函数与坐标轴的交点,然后作出函数图象即可;(3)根据函数图象与二次函数的增减性解答;(4)利用三角形的面积公式列式计算即可得解.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
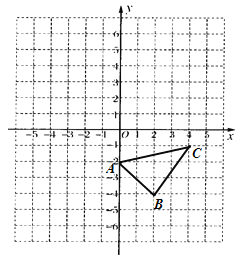
【题目】已知:如图,在平面直角坐标系中.
(1)作出△ABC关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 三个顶点的坐标:
三个顶点的坐标: ![]() ( ),
( ),![]() ( ),
( ),![]() ( );
( );
(2)直接写出△ABC的面积为 ;
(3)在![]() 轴上画点P,使PA+PC最小.
轴上画点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D为AB的中点,四边形BCED为平行四边形,DE,AC相交于F.连接DC,AE.
(1)试确定四边形ADCE的形状,并说明理由.
(2)若AB=16,AC=12,求四边形ADCE的面积.
(3)当△ABC满足什么条件时,四边形ADCE为正方形?请给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=120°,连接AC. 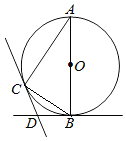
(1)求∠A的度数;
(2)若点D到BC的距离为2,那么⊙O的半径是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)2x2﹣8x=0.
(2)x2﹣3x﹣4=0.
求出抛物线的开口方向、对称轴、顶点坐标.
(3)y= ![]() x2﹣x+3(公式法).
x2﹣x+3(公式法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)如图,已知△ABC,∠C=Rt∠,AC<BC,D为BC上一点,且到A,B两点的距离相等.

(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,求∠CAD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com