练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形ABCD中，AD＝4，对角线AC与BD交于点O，OE⊥AC交BC于点E，CE＝3，则矩形ABCD的面积为（　　）

    A.B.C.12D.32

    【答案】B

    【解析】

    要求矩形的面积，已知一边的长度，所以只要把邻边的长度求出即可．因为矩形的对角线相互平分，所以点O是AC的中点，又因为OE垂直AC，所以OE是AC的垂直平分线，见到垂直平分线，我们应该想到垂直平分线的性质，根据垂直平分线的性质：垂直平分线上的点到线段两端距离相等，所以需要连接AE，可得AE=EC,再根据勾股定理可求出AB的长度，则矩形的面积就可以算出了．

    如图连接AE

    矩形的对角线相互平分

    O为AC的中点

    又 OE AC

    OE是AC的垂直平分线

    AE=EC=3,BE=BC-EC=AD-EC=1

    是直角三角形，由勾股定理可得：

    AB=

    矩形ABCD的面积=

    故本题选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在同一坐标系内，一次函数y＝ax＋b与二次函数y＝ax2＋8x＋b的图象可能是（ ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，AB∥CD，CF平分∠DCE，若∠DCF＝30°，∠E＝20°，求∠ABE的度数．

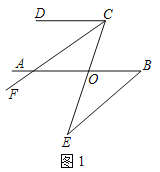
    （2）如图2，已知AB∥CD，CF平分∠DCE，∠EBF＝2∠ABF，若∠F的2倍与∠E的补角的和为190°，求∠ABE的度数．

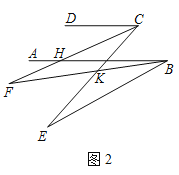
    （3）如图3，若P是（2）中的射线BE上一点，G是CD上任一点，PQ∥GN，PQ平分∠BPG，GM平分∠DGP，若∠B＝30°，求∠MGN的度数．

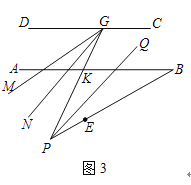
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用一根长22cm的铁丝：

    （1）能否围成面积是30cm2的扇形？若能，求出扇形半径；若不能，请说明理由．

    （2）能否围成面积是32cm2的扇形？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯，荣获了诺贝尔物理学奖．石墨烯目前是世上最薄却也是最坚硬的纳米材料，同时还是导电性最好的材料，其理论厚度仅0.000 000 000 34米，将这个数用科学记数法表示为

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的对角线AC与BD相交于点O，∠ACB的角平分线分别交AB、CD于M、N两点．若AM＝4，则BM＝_____，ON＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知y﹣2与x成正比例，当x＝2时，y＝6．

    （1）求y与x之间的函数解析式．

    （2）在所给直角坐标系中画出函数图象．

    （3）此函数图象与x轴交于点A，与y轴交于点B，点C在x轴上，若S△ABC＝3，请直接写出点C的坐标．

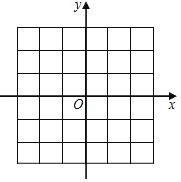
    查看答案和解析>>

    科目：初中数学 来源： 题型：

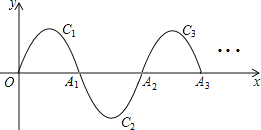
    【题目】如图，一段抛物线：y=﹣x（x﹣3）（0≤x≤3），记为C1，它与x轴交于点O，A1；将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3；…如此进行下去，直至得C17.

    （1）写出点的坐标________

    （2）若P（50，m）在第17段抛物线C17上，则m=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】4月的某天小欣在“A超市”买了“雀巢巧克力”和“趣多多小饼干”共10包，已知“雀巢巧克力”每包22元，“趣多多小饼干”每包2元，总共花费了80元．

    （1）请求出小欣在这次采购中，“雀巢巧克力”和“趣多多小饼干”各买了多少包？

    （2）“五一”期间，小欣发现，A、B两超市以同样的价格出售同样的商品，并且又各自推出不同的优惠方案：在A超市累计购物超过50元后，超过50元的部分打九折；在B超市累计购物超过100元后，超过100元的部分打八折．

    ①请问“五一”期间，若小欣购物金额超过100元，去哪家超市购物更划算？

    ②“五一”期间，小欣又到“B超市”购买了一些“雀巢巧克力”，请问她至少购买多少包时，平均每包价格不超过20元？

    查看答案和解析>>

    同步练习册答案