
| ���۷�ʽ | ֱ�ӳ��� | �ӹ��ɹ�ͷ���� |
| ����Ԫ/ǧ�ˣ� | 4 | 10 |
���� ��1��������30�����˽��в�ժ��ӹ�ˮ�����ӹ���ͷ�Ĺ���ÿ�˿ɼӹ�300ǧ�ˣ���ʾ���������ɣ�
�����üӹ�ˮ���������ܶ��ڲ�ժ�����ó�����ʽ��ϵ������ɣ�
��2����ʾ��ֱ�ӳ��ۺͼӹ�����������ó����ȹ�ϵ������ɣ�
��� �⣺��1���ټӹ���ͷ�Ĺ���Ϊ ��30-x���ˣ����Լӹ���ͷ 300��30-x��ǧ�ˣ����ú�x��ʽ�ӱ�ʾ��
�ʴ�Ϊ����30-x����300��30-x����
�����ժˮ���Ĺ���Ϊx�ˣ���������ɵã�
400x��300��30-x����
��ã�x��$\frac{90}{7}$=12$\frac{6}{7}$��
�𣺲�ժˮ���Ĺ�������13�ˣ�
��2����������Ϊw����w=4��[400x-300��30-x��]+10��300��30-x��=-200x+54000��
��ֱ�ӳ��������������������25%��
��4��[400x-300��30-x��]��25%��-200x+54000����
��ã�x��17$\frac{7}{19}$��
�ɢڵ�12$\frac{6}{7}$��x��17$\frac{7}{19}$��
��x=13ʱ��w���w=-200��13+54000=51400��Ԫ����
�𣺲�ժˮ���Ĺ���Ϊ13�ˣ��ӹ���ͷ�Ĺ�����17�ˣ��������Ϊ51400Ԫ��
���� ������Ҫ������һԪһ�β���ʽ��Ӧ�ã���������ֱ��ʾ���ӹ���������ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x=8}\\{y=-2}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x=9}\\{y=1}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 4����С��ͬ���������ľ�ڷų���ͼ��ʾ�ļ����壬������ͼ�ǣ�������
4����С��ͬ���������ľ�ڷų���ͼ��ʾ�ļ����壬������ͼ�ǣ�������| A�� | 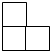 | B�� | 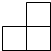 | C�� | 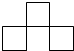 | D�� | 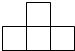 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
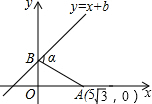 ��ͼ����֪��A��5$\sqrt{3}$��0����ֱ��y=x+b��b��0����y�ύ�ڵ�B������AB���Ϧ�=75�㣬��b=5��
��ͼ����֪��A��5$\sqrt{3}$��0����ֱ��y=x+b��b��0����y�ύ�ڵ�B������AB���Ϧ�=75�㣬��b=5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
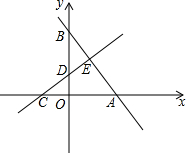 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ᡢy��ֱ��ڵ�A����B��ֱ��CD��x�ᡢy��ֱ��ڵ�C����D��AB��CD�ཻ�ڵ�E���߶�OA��OC�ij���һԪ���η���x2-18x+72=0��������OA��OC����BE=5��tan��ABO=$\frac{3}{4}$��
��ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ᡢy��ֱ��ڵ�A����B��ֱ��CD��x�ᡢy��ֱ��ڵ�C����D��AB��CD�ཻ�ڵ�E���߶�OA��OC�ij���һԪ���η���x2-18x+72=0��������OA��OC����BE=5��tan��ABO=$\frac{3}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
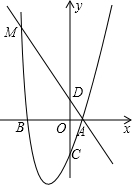 ��ͼ�����κ���y=x2+bx+c��ͼ��A��1��0����B��-3��0�����㣬��y�ύ�ڵ�C������A��ֱ����y�ύ�ɵ�D���������߽��ڵ�M����tan��BAM=1��
��ͼ�����κ���y=x2+bx+c��ͼ��A��1��0����B��-3��0�����㣬��y�ύ�ڵ�C������A��ֱ����y�ύ�ɵ�D���������߽��ڵ�M����tan��BAM=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
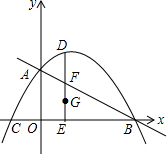 ��ͼ��������y=ax2+bx+2�������ύ��A��B��C���㣬����B��4��0����C��-2��0��������AB��AC���ڵ�һ�����ڵ�����������һ����D����D��DE��x�ᣬ����ΪE����AB�ڵ�F��
��ͼ��������y=ax2+bx+2�������ύ��A��B��C���㣬����B��4��0����C��-2��0��������AB��AC���ڵ�һ�����ڵ�����������һ����D����D��DE��x�ᣬ����ΪE����AB�ڵ�F���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com