
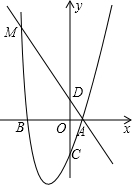
 ��ͼ�����κ���y=x2+bx+c��ͼ��A��1��0����B��-3��0�����㣬��y�ύ�ڵ�C������A��ֱ����y�ύ�ɵ�D���������߽��ڵ�M����tan��BAM=1��
��ͼ�����κ���y=x2+bx+c��ͼ��A��1��0����B��-3��0�����㣬��y�ύ�ڵ�C������A��ֱ����y�ύ�ɵ�D���������߽��ڵ�M����tan��BAM=1������ ��1��������֪����������������κ����Ľ���ʽ���������������ϵ�����Ӷ�ȷ�����κ����Ľ���ʽ��
��2��������õ�C�����꣬Ȼ�����Q������Ϊ��x��x2+2x+3��������S��QOC=4S��AOC���|x|=4���Ӷ����x��ֵ�������Q������⣻
��3����AE=PEʱ����AP=PEʱ����AP=AEʱ����������õ���ֱ�������ε��������P��-3��0����-2��-3����
���  �⣺��1�����κ���y=x2+bx+c��ͼ��A��1��0����B��-3��0�����㣬
�⣺��1�����κ���y=x2+bx+c��ͼ��A��1��0����B��-3��0�����㣬
��$\left\{\begin{array}{l}{1+b+c=0}\\{9=0-3b+c}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=2}\\{c=-3}\end{array}\right.$��
����κ����Ľ���ʽΪy=x2+2x-3��
��2����x=0��
��y=3��
��C��0��-3����
��OC=3��
���Q��������x��x2+2x-3����
��S��QOC=4S��AOC��
��$\frac{1}{2}$��3��|x|=4��$\frac{1}{2}$��3��1��
��|x|=4��
x=��4��
��x=4ʱ��x2+2x-3=16+8-3=21��
��x=-4ʱ��x2+2x-3=16-8-3=5��
���Q��������4��21����-4��5����
��3����Rt��AOD��
��tan��OAD=$\frac{OD}{OA}$=1��
��OD=OA��
���BAD=45�㣬
��������ۣ���AE=PEʱ��
�ߡ�APEΪ����ֱ�������Σ�
���EPA=��EAP=45�㣬
�ߡ�DAB=45�㣬
���ʱ��P���B�غϣ�
��P��-3��0����
�ڵ�AP=PEʱ�����PEA=��EAP=45�㣬
���EPA=90�㣬
��ʱ��P���B�غϣ�P��-3��0����
�۵�AP=AEʱ�����EAP=90�㣬
��AP��y�ύ�ڵ�F��
�ߡ�OAP=��OFA=45�㣬
��OA=OF=1��
��F��0��-1����
��ֱ��AP�Ľ���ʽΪy=kx+b����$\left\{\begin{array}{l}{0=k+b}\\{-1=b}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$��
��ֱ��AP�Ľ���ʽΪy=x-1��
��P��x��x2+2x-3����
��x2+2x-3=x-1��
��ã�x=1���������⣩��x=-2��
��P��-2��-3����
����������P��-3��0����-2��-3����
���� �����Ƕ��κ������ۺ����ͣ������漰����֪ʶ���������ߵĶ��㹫ʽ�������ε�����������йض�������ʱҪע����������������۽����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���۷�ʽ | ֱ�ӳ��� | �ӹ��ɹ�ͷ���� |
| ����Ԫ/ǧ�ˣ� | 4 | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
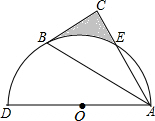 ��ͼ����ADΪֱ���İ�ԲO����Rt��ABCб��AB�������˵㣬��ֱ�DZ�AC�ڵ�E����B��Eǡ���ǰ�Բ�������ȷֵ㣮��AD=4����ͼ����Ӱ���ֵ����Ϊ$\frac{3\sqrt{3}}{2}$-$\frac{2��}{3}$��
��ͼ����ADΪֱ���İ�ԲO����Rt��ABCб��AB�������˵㣬��ֱ�DZ�AC�ڵ�E����B��Eǡ���ǰ�Բ�������ȷֵ㣮��AD=4����ͼ����Ӱ���ֵ����Ϊ$\frac{3\sqrt{3}}{2}$-$\frac{2��}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x-2y | B�� | x+2y | C�� | -x-2y | D�� | -x+2y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
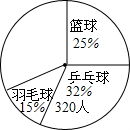 Ϊ���˽�ijУѧ��������������ë��ƹ��������������ϲ����С������˳������飬�ڻ�������ͼʱ������ʱ��ִ٣����������������Ϣ��û�л�����ɣ���ͼ��ʾ������ͼ�е���Ϣ�����������������ѧ����ϲ������������������ǣ�������
Ϊ���˽�ijУѧ��������������ë��ƹ��������������ϲ����С������˳������飬�ڻ�������ͼʱ������ʱ��ִ٣����������������Ϣ��û�л�����ɣ���ͼ��ʾ������ͼ�е���Ϣ�����������������ѧ����ϲ������������������ǣ�������| A�� | 100�� | B�� | 200�� | C�� | 260�� | D�� | 400�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
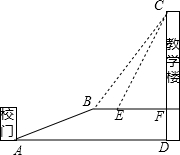 ������һ��������ɽ�£�ij��ѧ��ɽ������У��A������һб��AB������Ϊ13�ף����¶�B������ѧ¥CF��¥��C�����ǡ�CBF=53�㣬��B��4��Զ��E����һ��̨����E������C�����ǡ�CEF=63.4�㣬CF���ӳ��߽�У�Ŵ���ˮƽ����D�㣬FD=5�ף�
������һ��������ɽ�£�ij��ѧ��ɽ������У��A������һб��AB������Ϊ13�ף����¶�B������ѧ¥CF��¥��C�����ǡ�CBF=53�㣬��B��4��Զ��E����һ��̨����E������C�����ǡ�CEF=63.4�㣬CF���ӳ��߽�У�Ŵ���ˮƽ����D�㣬FD=5�ף��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com