
分析 先算括号内的减法,把除法变成乘法,算乘法,最后代入求出即可.
解答 解:$({x+1-\frac{3x}{{{x^2}-x}}})÷({\frac{x^2}{x-1}-4})$
=[$\frac{x+1}{1}$-$\frac{3x}{x(x-1)}$]÷[$\frac{{x}^{2}}{x-1}$-$\frac{4(x-1)}{x-1}$]
=$\frac{{x}^{2}-4}{x-1}$÷$\frac{{x}^{2}-4x+4}{x-1}$
=$\frac{(x+2)(x-2)}{x-1}$•$\frac{x-1}{(x-2)^{2}}$
=$\frac{x+2}{x-2}$,
当x=2-$\sqrt{2}$时,原式=$\frac{4-\sqrt{2}}{-\sqrt{2}}$=1-2$\sqrt{2}$.
点评 此题考查了分式的化简求值和二次根式的混合运算的应用,熟练掌握运算法则是解本题的关键,注意运算顺序.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=8}\\{y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=9}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 2 | 2 | 4 | 3 | 3 | 2 |
| A. | 4 | B. | 1.75 | C. | 1.70 | D. | 1.65 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
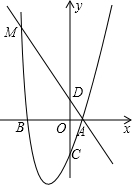 如图,二次函数y=x2+bx+c的图象经过A(1,0),B(-3,0)两点,与y轴交于点C,过点A的直线与y轴交干点D,与抛物线交于点M,且tan∠BAM=1.
如图,二次函数y=x2+bx+c的图象经过A(1,0),B(-3,0)两点,与y轴交于点C,过点A的直线与y轴交干点D,与抛物线交于点M,且tan∠BAM=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com