
【题目】正方形ABCD,点E为AB的中点,且BF=![]() BC.
BC.
(1)如图1,求证:DE⊥EF.
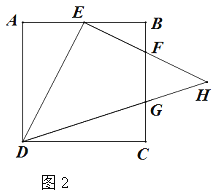
(2)如图2,若点G在BC上,且CD=3CG,DG、EF交于H点,求![]() 的值.
的值.

【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接DF,设BF=a,利用勾股定理用a表示出DE、EF、DF的长,然后根据勾股定理的逆定理即可得出结论;
(2)连接EG,延长BC至M,使CM=AE,连接DM,可得△DAE≌△DCM,得出DE=DM,∠ADE=∠CDM,推出∠EDM=90°,然后利用勾股定理分别用a表示EG和MG,证出EG=MG,利用SSS可证得△DGE≌△DGM,进而证得∠EDH=45°,利用勾股定理求出DH,即可得出![]() 的值.
的值.
(1)连接DF,设BF=a,则CF=3a,AD=CD=4a,AE=BE=2a,
由勾股定理得:DF=5a,DE= 2![]() a,EF=
a,EF=![]() a,
a,
∴DE2+EF2=( 2![]() a)2+(
a)2+(![]() a)2=25a2,DF2=25a2,
a)2=25a2,DF2=25a2,
∴DE2+EF2=DF2,
∴∠DEF=90,
∴DE⊥EF;
(2)连接EG,延长BC至M,使CM=AE,连接DM,
在△DAE和△DCM中,
 ,
,
∴△DAE≌△DCM(SAS),
∴DE=DM,∠ADE=∠CDM,
∴∠EDM=∠ADC=90°,
∵CD=3CG,
∴CG=![]() a,
a,
∴MG=MC+CG=2a+![]() a=
a=![]() a,
a,
在RtΔBEG中,由勾股定理得:EG=![]() a,
a,
∴EG=MG,
∴△DGE≌△DGM(SSS),
∴∠EDG=∠MDG=45°,
∴△EDH是等腰直角三角形,
∴DH=![]() DE=
DE=![]() EH,
EH,
∴![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠BAC=90°,D是AC的中点,CE⊥BD于点E,交BA的延长线于点F.若BF=12,则△FBC的面积为( )

A. 40 B. 46 C. 48 D. 50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车从停车场出发,沿着东西向的大街行驶,到晚上6时,一天的行驶记录如下:(向东行驶记为正,向西行驶记为负,单位:千米)-4、+7、-9、+8、+6、-4、-3、+12
(1)到晚上6时,出租车在什么位置?
(2)若汽车每千米耗油0.2升,则从停车场出发到晚上6时,出租车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在扇形BAD中,点C在 ![]() 上,且∠BDC=30°,AB=2
上,且∠BDC=30°,AB=2 ![]() ,∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )
,∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( ) 
A.π﹣2
B.π﹣1
C.2π﹣2
D.2π+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AC=16,则图中长度为8的线段有( )

A. 2条 B. 4条 C. 5条 D. 6条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上 A、B 两点所对应的数分别是 a 和 b,且(a+5)2+|b﹣7|=0.
(1)求 a,b;A、B 两点之间的距离.
(2)有一动点 P 从点 A 出发第一次向左运动 1 个单位长度,然后在新的位置第二次运动,向右运动 2个单位长度,在此位置第三次运动,向左运动 3个单位长度…按照如此规律不断地左右运动,当运动到 2019次时,求点P所对应的数.
(3)在(2)的条件下,点 P在某次运动时恰好到达某一个位置,使点 P到点B的距离是点 P 到点 A 的距离的3倍?请直接写出此时点 P所对应的数,并分别写出是第几次运动.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com