
【题目】如图所示,在扇形BAD中,点C在 ![]() 上,且∠BDC=30°,AB=2
上,且∠BDC=30°,AB=2 ![]() ,∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )
,∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( ) 
A.π﹣2
B.π﹣1
C.2π﹣2
D.2π+1
科目:初中数学 来源: 题型:
【题目】某文具店老板第一次用1000元购进一批文具,很快销售完毕;第二次购进时发现每件文具进价比第一次上涨了2.5元.老板用2500元购进了第二批文具,所购进文具的数量是第一次购进数量的2倍,同样很快销售完毕,两批文具的售价为每件15元.
(1)问第二次购进了多少件文具?
(2)文具店老板第一次购进的文具有30元的损耗,第二次购进的文具有125元的损耗,问文具店老板在这两笔生意中是盈利还是亏本?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD,点E为AB的中点,且BF=![]() BC.
BC.
(1)如图1,求证:DE⊥EF.
(2)如图2,若点G在BC上,且CD=3CG,DG、EF交于H点,求![]() 的值.
的值.

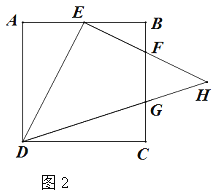
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当前正值樱桃销售季节,小李用20000元在樱桃基地购进樱桃若干进行销售,由于销售状况良好,他又立即拿出60000元资金购进该种樱桃,但这次的进货价比第一次的进货价提高了20%,购进樱桃数量是第一次的2倍还多200千克.
(1)该种樱桃的第一次进价是每千克多少元?
(2)如果小李按每千克90元的价格出售,当大部分樱桃售出后,余下500千克按售价的7折出售完,小李销售这种樱桃共盈利多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设计一个商标图形(如图8所示),在△ABC中,AB=AC=2cm,∠B=30°,以A为圆心,AB为半径作 ![]() ,以BC为直径作半圆
,以BC为直径作半圆 ![]() ,则商标图案(阴影)面积等于cm2 .
,则商标图案(阴影)面积等于cm2 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com