
【题目】如图,□ABCD,BE//DF,且分别交对角线AC于点E,F,连接ED,BF .
求证:(1)ΔABE≌ΔCDF;
(2)∠DEF=∠BFE.
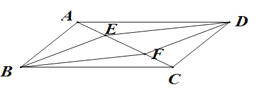
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)首先由平行四边形的性质可得AB=CD,AB∥CD,再根据平行线的性质可得∠BAE=∠DCF,∠BEC=∠DFA,即可根据AAS定理判定△ABE≌△CDF;
(2)只要证明四边形BEDF是平行四边形,推出DE∥BF即可证明.
证明:(1)在□ABCD中,
AB=CD,AB∥CD,
∴∠BAC=∠DCA,
又∵BE∥DF,
∴∠BEF=∠DFE,
∴∠AEB=∠CFD,
在△ABE和△CDF中,
∵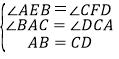 ,
,
∴ΔABE≌ΔCDF(AAS);
(2)由(1)知,BE=DF,
又∵BE∥DF,
∴四边形BEDF是平行四边形,
∴DE∥BF,
∴∠DEF=∠BFE.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1 , S2 , S3 , …,S10 , 则S1+S2+S3+…+S10= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( ) 
A.94分,96分
B.96分,96分
C.94分,96.4分
D.96分,96.4分
查看答案和解析>>
科目:初中数学 来源: 题型:
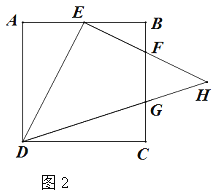
【题目】正方形ABCD,点E为AB的中点,且BF=![]() BC.
BC.
(1)如图1,求证:DE⊥EF.
(2)如图2,若点G在BC上,且CD=3CG,DG、EF交于H点,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;② ![]() ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN= ![]() PC.其中正确的个数是( )
PC.其中正确的个数是( ) 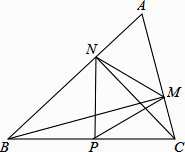
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒4个单位长度的速度向终点C移动,设移动时间为t秒.
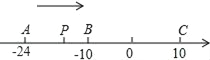
(1)用含t的代数式表示点P与A的距离:PA= ;点P对应的数是 ;
(2)动点Q从点B出发,以每秒1个单位长度的速度向终点C移动,若P、Q同时出发,求:当点P运动多少秒时,点P和点Q间的距离为8个单位长度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com