
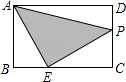
【题目】如图,在矩形ABCD中,AB=2,AD=3,BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是
( )
A.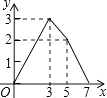
B.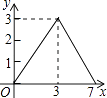
C.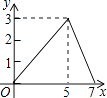
D.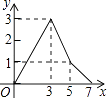
【答案】A
【解析】∵在矩形ABCD中,AB=2,AD=3,
∴CD=AB=2,BC=AD=3,
∵BE=1,
∴CE=BC﹣BE=2,①点P在AD上时,△APE的面积y= ![]() x2=x(0≤x≤3),②点P在CD上时,S△APE=S梯形AECD﹣S△ADP﹣S△CEP,
x2=x(0≤x≤3),②点P在CD上时,S△APE=S梯形AECD﹣S△ADP﹣S△CEP,
= ![]() (2+3)×2﹣
(2+3)×2﹣ ![]() ×3×(x﹣3)﹣
×3×(x﹣3)﹣ ![]() ×2×(3+2﹣x),
×2×(3+2﹣x),
=5﹣ ![]() x+
x+ ![]() ﹣5+x,
﹣5+x,
=﹣ ![]() x+
x+ ![]() ,
,
∴y=﹣ ![]() x+
x+ ![]() (3<x≤5),③点P在CE上时,S△APE=
(3<x≤5),③点P在CE上时,S△APE= ![]() ×(3+2+2﹣x)×2=﹣x+7,
×(3+2+2﹣x)×2=﹣x+7,
∴y=﹣x+7(5<x≤7),
所以答案是:A.
【考点精析】利用一次函数的图象和性质对题目进行判断即可得到答案,需要熟知一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.


科目:初中数学 来源: 题型:
【题目】将五个边长都为2cm的正方形按如图所示摆放,点A,B,C,D分别是四个正方形的中心(对角线的交点),则图中四块阴影面积的和为( )
A.2cm2
B.4cm2
C.6cm2
D.8cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知□ABCD,AB∥x轴,AB=6,点A的坐标为(1,﹣4),点D的坐标为(﹣3,4),点B在第四象限,点P是□ABCD边上的一个动点.
(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x﹣1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标.(直接写出答案)
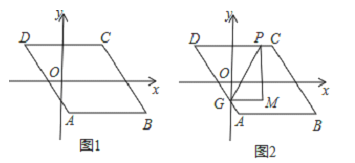
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com