
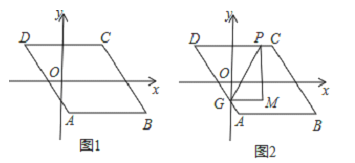
”¾ĢāÄæ”æČēĶ¼1£¬ŅŃÖŖ”õABCD£¬AB”ĪxÖį£¬AB=6£¬µćAµÄ×ų±źĪŖ£Ø1£¬©4£©£¬µćDµÄ×ų±źĪŖ£Ø©3£¬4£©£¬µćBŌŚµŚĖÄĻóĻŽ£¬µćPŹĒ”õABCD±ßÉĻµÄŅ»øö¶Æµć£®
£Ø1£©ČōµćPŌŚ±ßBCÉĻ£¬PD=CD£¬ĒóµćPµÄ×ų±ź£®
£Ø2£©ČōµćPŌŚ±ßAB£¬ADÉĻ£¬µćP¹ŲÓŚ×ų±źÖį¶Ō³ĘµÄµćQĀäŌŚÖ±Ļßy=x©1ÉĻ£¬ĒóµćPµÄ×ų±ź£®
£Ø3£©ČōµćPŌŚ±ßAB£¬AD£¬CDÉĻ£¬µćGŹĒADÓėyÖįµÄ½»µć£¬ČēĶ¼2£¬¹żµćP×÷yÖįµÄĘ½ŠŠĻßPM£¬¹żµćG×÷xÖįµÄĘ½ŠŠĻßGM£¬ĖüĆĒĻą½»ÓŚµćM£¬½«”÷PGMŃŲÖ±ĻßPG·ÕŪ£¬µ±µćMµÄ¶ŌÓ¦µćĀäŌŚ×ų±źÖįÉĻŹ±£¬ĒóµćPµÄ×ų±ź£®£ØÖ±½ÓŠ“³ö“š°ø£©
”¾“š°ø”æ£Ø1£©µćP×ų±źĪŖ£Ø3£¬4£©£»£Ø2£©µćPµÄ×ų±źĪŖ£Ø©3£¬4£©»ņ£Ø©1£¬0£©»ņ£Ø5£¬©4£©»ņ£Ø3£¬©4£©£»£Ø3£©µćP×ų±źĪŖ£Ø2£¬©4£©»ņ£Ø©![]() £¬3£©»ņ£Ø©
£¬3£©»ņ£Ø©![]() £¬4£©»ņ£Ø
£¬4£©»ņ£Ø![]() £¬4£©£®
£¬4£©£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©µćPŌŚBCÉĻ£¬ŅŖŹ¹PD=CD£¬Ö»ÓŠPÓėCÖŲŗĻ£»
£Ø2£©Ź×ĻČŅŖ·ÖµćPŌŚ±ßAB£¬ADÉĻŹ±ĢÖĀŪ£¬øł¾Ż”°µćP¹ŲÓŚ×ų±źÖį¶Ō³ĘµÄµćQ”±£¬¼“»¹ŅŖĻø·Ö”°µćP¹ŲÓŚxÖįµÄ¶Ō³ĘµćQŗĶµćP¹ŲÓŚyÖįµÄ¶Ō³ĘµćQ”±ĢÖĀŪ£¬øł¾Ż¹ŲÓŚxÖį”¢yÖį¶Ō³ĘµćµÄĢŲÕ÷£Ø¹ŲÓŚxÖį¶Ō³ĘŹ±£¬µćµÄŗį×ų±ź²»±ä£¬×Ż×ų±ź±ä³ÉĻą·“Źż£»¹ŲÓŚyÖį¶Ō³ĘŹ±£¬Ļą·“£»£©½«µĆµ½µÄµćQµÄ×ų±ź“śČėÖ±Ļßy=x-1£¬¼“æɽā“š£»
£Ø3£©ŌŚ²»Ķ¬±ßÉĻ£¬øł¾ŻĶ¼Ļ󣬵ćM·ÕŪŗ󣬵ćM”ÆĀäŌŚxÖį»¹ŹĒyÖį£¬æÉŌĖÓĆĻąĖĘĒó½ā£®
ŹŌĢā½āĪö£ŗ£Ø1£©”ßCD=6£¬”ąµćPÓėµćCÖŲŗĻ£¬”ąµćPµÄ×ų±źŹĒ£Ø3£¬4£©£®
£Ø2£©¢Łµ±µćPŌŚ±ßADÉĻŹ±£¬ÓÉŅŃÖŖµĆ£¬Ö±ĻßADµÄŗÆŹż±ķ“ļŹ½ĪŖ£ŗ![]() £¬ÉčP£Øa£¬-2a-2£©£¬ĒŅ-3”Üa”Ü1£®
£¬ÉčP£Øa£¬-2a-2£©£¬ĒŅ-3”Üa”Ü1£®
ČōµćP¹ŲÓŚxÖį¶Ō³ĘµćQ1£Øa£¬2a+2£©ŌŚÖ±Ļßy=x-1ÉĻ£¬”ą2a+2=a-1£¬½āµĆa=-3£¬“ĖŹ±P£Ø-3£¬4£©£®
ČōµćP¹ŲÓŚyÖį¶Ō³ĘµćQ2£Ø-a£¬-2a-2£©ŌŚÖ±Ļßy=x-1ÉĻ£¬”ą-2a-2=-a-1£¬½āµĆa=-1£¬“ĖŹ±P£Ø-1£¬0£©£®
¢Śµ±µćPŌŚ±ßABÉĻŹ±£¬ÉčP£Øa£¬-4£©£¬ĒŅ1”Üa”Ü7£®
ČōµćP¹ŲÓŚxÖį¶Ō³ĘµćQ3£Øa£¬4£©ŌŚÖ±Ļßy=x-1ÉĻ£¬”ą4=a-1£¬½āµĆa=5£¬“ĖŹ±P£Ø5£¬-4£©£®
ČōµćP¹ŲÓŚyÖį¶Ō³ĘµćQ4£Ø-a£¬-4£©ŌŚÖ±Ļßy=x-1ÉĻ£¬”ą-4=-a-1£¬½āµĆa=3£¬“ĖŹ±P£Ø3£¬-4£©£®
×ŪÉĻĖłŹö£¬µćPµÄ×ų±źĪŖ£Ø-3£¬4£©»ņ£Ø-1£¬0£©»ņ£Ø5£¬-4£©»ņ£Ø3£¬-4£©£®
£Ø3£©ŅņĪŖÖ±ĻßADĪŖy=-2x-2£¬ĖłŅŌG£Ø0£¬-2£©£®
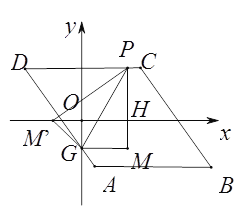
¢ŁČēĶ¼£¬µ±µćPŌŚCD±ßÉĻŹ±£¬æÉÉčP£Øm£¬4£©£¬ĒŅ-3”Üm”Ü3£¬ŌņæɵĆM”äP=PM=4+2=6£¬M”äG=GM=|m|£¬Ņ×Ö¤µĆ”÷OGM”ä”×”÷HM”äP£¬Ōņ![]() £¬¼“
£¬¼“![]() £¬ŌņOM”ä=
£¬ŌņOM”ä=![]() £¬ŌŚRt”÷OGM”äÖŠ£¬Óɹ“¹É¶ØĄķµĆ£¬
£¬ŌŚRt”÷OGM”äÖŠ£¬Óɹ“¹É¶ØĄķµĆ£¬![]() £¬½āµĆm=-
£¬½āµĆm=-![]() »ņ
»ņ![]() £¬ŌņP£Ø-
£¬ŌņP£Ø-![]() £¬4£©»ņ£Ø
£¬4£©»ņ£Ø![]() £¬4£©£»
£¬4£©£»
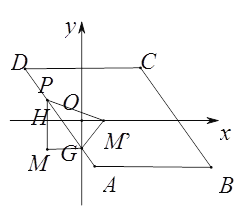
¢ŚČēĻĀĶ¼£¬µ±µćPŌŚAD±ßÉĻŹ±£¬ÉčP£Øm£¬-2m-2£©£¬ŌņPM”ä=PM=|-2m|£¬GM”ä=MG=|m|£¬Ņ×Ö¤µĆ”÷OGM”ä”×”÷HM”äP£¬Ōņ![]() £¬¼“
£¬¼“![]() £¬ŌņOM”ä=
£¬ŌņOM”ä=![]() £¬ŌŚRt”÷OGM”äÖŠ£¬Óɹ“¹É¶ØĄķµĆ£¬
£¬ŌŚRt”÷OGM”äÖŠ£¬Óɹ“¹É¶ØĄķµĆ£¬![]() £¬ÕūĄķµĆm= -
£¬ÕūĄķµĆm= -![]() £¬ŌņP£Ø-
£¬ŌņP£Ø-![]() £¬3£©£»
£¬3£©£»
ČēĻĀĶ¼£¬µ±µćPŌŚAB±ßÉĻŹ±£¬ÉčP£Øm£¬-4£©£¬“ĖŹ±M”äŌŚyÖįÉĻ£¬ŌņĖıߊĪPM”äGMŹĒÕż·½ŠĪ£¬ĖłŅŌGM=PM=4-2=2£¬ŌņP£Ø2£¬-4£©£®
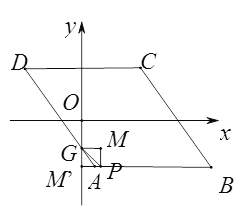
×ŪÉĻĖłŹö£¬µćPµÄ×ų±źĪŖ£Ø2£¬-4£©»ņ£Ø-![]() £¬3£©»ņ£Ø-
£¬3£©»ņ£Ø-![]() £¬4£©»ņ£Ø
£¬4£©»ņ£Ø![]() £¬4£©£®
£¬4£©£®


 ŗ®¼ŁĢģµŲÖŲĒģ³ö°ęÉēĻµĮŠ“š°ø
ŗ®¼ŁĢģµŲÖŲĒģ³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻČ»Æ¼ņŌŁĒóÖµ£ŗ£Ø2a+b£©£Øb-2a£©-£Øa-3b£©2£¬ĘäÖŠa=-1£¬b=2£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČē¹ūa£¬b»„ĪŖĻą·“Źż£¬c£¬d»„ĪŖµ¹Źż£¬xµÄ¾ų¶ŌÖµµČÓŚ2£¬ÄĒĆ“x2+cdx©a©bµÄÖµŹĒ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬AB=2£¬AD=3£¬BE=1£¬¶ÆµćP“ÓµćA³ö·¢£¬ŃŲĀ·¾¶A”śD”śC”śEŌĖ¶Æ£¬Ōņ”÷APEµÄĆ껿yÓėµćP¾¹żµÄĀ·¾¶³¤xÖ®¼äµÄŗÆŹż¹ŲĻµÓĆĶ¼Ļó±ķŹ¾“óÖĀŹĒ
£Ø £©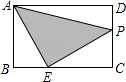
A.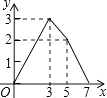
B.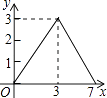
C.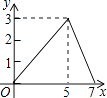
D.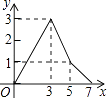
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£ĪŖĮĖ½ā°ĖÄź¼¶Ń§ÉśµÄŹÓĮ¦Ēéæö£¬¶Ō°ĖÄź¼¶µÄѧɜ½ųŠŠĮĖŅ»“ĪŹÓĮ¦µ÷²é£¬²¢½«µ÷²éŹż¾Ż½ųŠŠĶ³¼ĘÕūĄķ£¬»ęÖĘ³öČēĻĀʵŹż·Ö²¼±ķŗĶʵŹż·Ö²¼Ö±·½Ķ¼µÄŅ»²æ·Ö£®
ŹÓĮ¦ | ʵŹż£ØČĖ£© | ʵĀŹ |
4.0”Üx£¼4.3 | 20 | 0.1 |
4.3”Üx£¼4.6 | 40 | 0.2 |
4.6”Üx£¼4.9 | 70 | 0.35 |
4.9”Üx£¼5.2 | a | 0.3 |
5.2”Üx£¼5.5 | 10 | b |
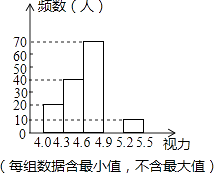
£Ø1£©ŌŚĘµŹż·Ö²¼±ķÖŠ£¬a= £¬ b=£»
£Ø2£©½«ĘµŹż·Ö²¼Ö±·½Ķ¼²¹³äĶźÕū£»
£Ø3£©ČōŹÓĮ¦ŌŚ4.6ŅŌÉĻ£Øŗ¬4.6£©¾łŹōÕż³££¬ĒóŹÓĮ¦Õż³£µÄČĖŹżÕ¼±»µ÷²éČĖŹżµÄ°Ł·Ö±ČŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ÓŠŅ»øö±ß³¤²»¶ØµÄÕż·½ŠĪABCD£¬ĖüµÄĮ½øöĻą¶ŌµÄ¶„µćA£¬C·Ö±šŌŚ±ß³¤ĪŖ1µÄÕżĮł±ßŠĪŅ»×éĘ½ŠŠµÄ¶Ō±ßÉĻ£¬ĮķĶāĮ½øö¶„µćB£¬DŌŚÕżĮł±ßŠĪÄŚ²æ£Ø°üĄØ±ß½ē£©£¬ŌņÕż·½ŠĪ±ß³¤aµÄȔֵ·¶Ī§ŹĒ £®
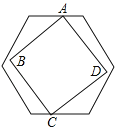
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬”ĻC£½90”ć£¬AC£½3£¬AB£½5£¬ČōŅŌA”¢B”¢C”¢PĖĵćĪŖ¶„µć×é³ÉŅ»øöĘ½ŠŠĖıߊĪ£¬ŌņÕāøöĘ½ŠŠĖıߊĪµÄÖܳ¤ĪŖ_____”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø±¾Ģā10·Ö£©ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AC=BC£¬”ĻACB=90”ć£¬”ŃO£ØŌ²ŠÄOŌŚ”÷ABCÄŚ²æ£©¾¹żB”¢CĮ½µć£¬½»ABÓŚµćE£¬¹żµćE×÷”ŃOµÄĒŠĻß½»ACÓŚµćF£®ŃÓ³¤CO½»ABÓŚµćG£¬×÷ED”ĪAC½»CGÓŚµćD
£Ø1£©ĒóÖ¤£ŗĖıߊĪCDEFŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©ČōBC=3£¬tan”ĻDEF=2£¬ĒóBGµÄÖµ£®

²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com