
【题目】甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.
(1)若开始时球在甲手中,求经过三次传球后,球传回到甲手中的概率是多少?
(2)若丙想使球经过三次传递后,球落在自己手中的概率最大,丙会让球开始时在谁手中?请说明理由.
【答案】
(1)解:画树状图如图所示,
三次传球有8种等可能结果,其中传回甲手中的有2种,即甲→乙→丙→甲,甲→丙→乙→甲,
∴经过三次传球后,球传回到甲手中的概率为 ![]() =
= ![]() .
.

(2)解:由树状图可知:从甲开始传球,传球三次后传到丙手中的概率为 ![]() ,
,
同理:从乙开始传球,传球三次后传到丙手中的概率为 ![]() ,从丙自己开始传球,传球三次后传到丙手中的概率为
,从丙自己开始传球,传球三次后传到丙手中的概率为 ![]() =
= ![]() ,
,
∴丙想使球经过三次传递后,球落在自己手中的概率最大,丙会让球开始时在甲或乙手中.
【解析】(1)依照题意画出树状图,根据树状图即可得出经过三次传球后球传回到甲手中的概率;(2)结合(1)的树状图,可得出从甲开始传球传球三次后传到丙手中的概率,同理,可得出从乙、丙开始传球,三次传球后传到丙手中的概率,对比后即可得出结论.
【考点精析】关于本题考查的列表法与树状图法,需要了解当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是( ) 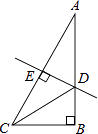
A.2 ![]()
B.2
C.4 ![]()
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:AD与⊙O相切于点D,AF经过圆心与圆交于点E、F,连接DE、DF,且EF=6,AD=4. 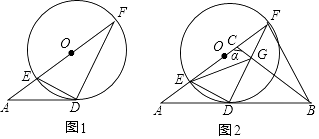
(1)证明:AD2=AEAF;
(2)延长AD到点B,使DB=AD,直径EF上有一动点C,连接CB交DF于点G,连接EG,设∠ACB=α,BG=x,EG=y. ①当α=900时,探索EG与BD的大小关系?并说明理由;
②当α=1200时,求y与x的关系式,并用x的代数式表示y.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在Rt△ABC中,斜边AB=10,sinA= ![]() ,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,QN⊥CP于N.
,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,QN⊥CP于N.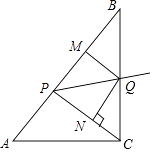
(1)当AP=CP时,求QP;
(2)若四边形PMQN为菱形,求CQ;
(3)探究:AP为何值时,四边形PMQN与△BPQ的面积相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550﹣1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707﹣1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若ax=N(a>0,a≠1),那么x叫做以a为底N的对数,记作:x=logaN.比如指数式24=16可以转化为4=log216,对数式2=log525可以转化为52=25.
我们根据对数的定义可得到对数的一个性质:loga(MN)=logaM+logaN(a>0,a≠1,M>0,N>0);理由如下:
设logaM=m,logaN=n,则M=am,N=an
∴MN=aman=am+n,由对数的定义得m+n=loga(MN)
又∵m+n=logaM+logaN
∴loga(MN)=logaM+logaN
解决以下问题:
(1)将指数43=64转化为对数式_____;
(2)证明loga![]() =logaM﹣logaN(a>0,a≠1,M>0,N>0)
=logaM﹣logaN(a>0,a≠1,M>0,N>0)
(3)拓展运用:计算log32+log36﹣log34=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,∠B=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.
(1)如果点D在线段BC上运动,如图1:
①依题意补全图1;
②求证:∠BAD=∠EDC;
③通过观察、实验,小明得出结论:在点D运动的过程中,总有∠DCE=135°,.
小明与同学讨论后,形成了证明这个结论的几种想法:
想法一:在AB上取一点F,使得BF=BD,要证∠DCE=135°,只需证△ADF≌△DEC.
想法二:以点D为圆心,DC为半径画弧交AC于点F,要证∠DCE=135°,只需证△AFD≌△DCE.
想法三:过点E作BC所在直线的垂直线段EF,要证∠DCE=135°,只需证EF=CF.
…
请你参考上面的想法,证明∠DCE=135°
(2)如果点D在线段CB的延长线上运动,利用图2画图分析,∠DCE的度数还是确定的值吗?如果是,直接写出∠DCE的度数;如果不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABF中,以AB为直径的圆分别交边AF、BF于C、E两点,CD⊥AF.AC是∠DAB的平分线, 
(1)求证:直线CD是⊙O的切线.
(2)求证:△FEC是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com