
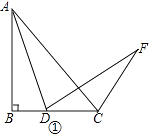
【题目】在△ABC中,AB=BC,∠B=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.
(1)如果点D在线段BC上运动,如图1:
①依题意补全图1;
②求证:∠BAD=∠EDC;
③通过观察、实验,小明得出结论:在点D运动的过程中,总有∠DCE=135°,.
小明与同学讨论后,形成了证明这个结论的几种想法:
想法一:在AB上取一点F,使得BF=BD,要证∠DCE=135°,只需证△ADF≌△DEC.
想法二:以点D为圆心,DC为半径画弧交AC于点F,要证∠DCE=135°,只需证△AFD≌△DCE.
想法三:过点E作BC所在直线的垂直线段EF,要证∠DCE=135°,只需证EF=CF.
…
请你参考上面的想法,证明∠DCE=135°
(2)如果点D在线段CB的延长线上运动,利用图2画图分析,∠DCE的度数还是确定的值吗?如果是,直接写出∠DCE的度数;如果不是,说明理由.
【答案】
(1)
解:①如图①所示;
②证明:∵∠B=90°,
∴∠BAD+∠BDA=90°,
∵∠ADE=90°,点D在线段BC上,
∴∠BAD+∠EDC=90°,
∴∠BAD=∠EDC;
②证法1:如图1,在AB上取点F,使得BF=BD,连接DF,
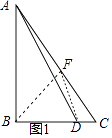
∵BF=BD,∠B=90°,
∴∠BFD=45°,
∴∠AFD=135°,
∵BA=BC,
∴AF=CD,
在△ADF和△DEC中,
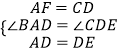 ,
,
∴△ADF≌△DEC,
∴∠DCE=∠AFD=135°;
证法2:以D为圆心,DC为半径作弧交AC于点F,连接DF,
∴DC=DF,∠DFC=∠DCF,
∵∠B=90°,AB=BC,
∴∠ACB=45°,∠DFC=45°,
∴∠DFC=90°,∠AFD=135°,
∵∠ADE=∠FDC=90°,
∴∠ADF=∠EDC,
在△ADF≌△CDE中, 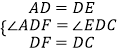 ,
,
∴△ADF≌△CDE,
∴∠AFD=∠DCE=135°;
证法3:过点E作EF⊥BC交BC的延长线于点F,
∴∠EFD=90°,
∵∠B=90°,
∴∠EFD=∠B,
在△ABD和△DFE中, 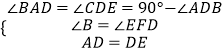 ,
,
∴△ABD≌△DFE,
∴AB=DF,BD=EF,
∵AB=BC,
∴BC=DF,BC﹣DC=DF﹣DC,
即BD=CF,
∴EF=CF,
∵∠EFC=90°,
∴∠ECF=45°,∠DCE=135°;
(2)
解:解:∠DCE=45°,
理由:过E作EF⊥DC于F,
∵∠ABD=90°,
∴∠EDF=∠DAB=90°﹣∠ADB,
在△ABD和△DFE中, 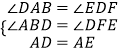 ,
,
∴△ABD≌△DFE,
∴DB=EF,AB=DF=BC,
∴BC﹣BF=DF﹣BF,
即FC=DB,
∴FC=EF,
∴∠DCE=45°.
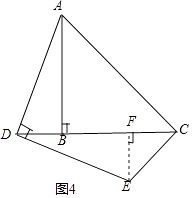
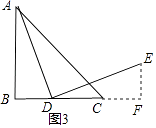
【解析】(1)①根据题意作出图形即可;②根据余角的性质得到结论;③证法1:如图1,在AB上取点F,使得BF=BD,连接DF,根据等腰直角三角形的性质得到∠BFD=45°,根据全等三角形的性质得到∠DCE=∠AFD=135°;证法2:以D为圆心,DC为半径作弧交AC于点F,连接DF,根据全等三角形的性质即可得到结论;证法3:过点E作EF⊥BC交BC的延长线于点F,根据全等三角形的性质即可得到结论;(2)过E作EF⊥DC于F,根据全等三角形的性质得到DB=EF,AB=DF=BC,根据线段的和差得到FC=EF,于是得到结论.
【考点精析】利用全等三角形的性质和旋转的性质对题目进行判断即可得到答案,需要熟知全等三角形的对应边相等; 全等三角形的对应角相等;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案科目:初中数学 来源: 题型:
【题目】2017年3月全国两会胜利召开,某学校就两会期间出现频率最高的热词:A.蓝天保卫战,B.不动产保护,C.经济增速,D.简政放权等进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题: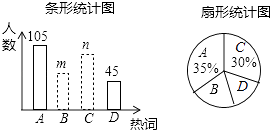
(1)本次调查中,一共调查了名同学;
(2)条形统计图中,m= , n=;
(3)从该校学生中随机抽取一个最关注热词D的学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.
(1)若开始时球在甲手中,求经过三次传球后,球传回到甲手中的概率是多少?
(2)若丙想使球经过三次传递后,球落在自己手中的概率最大,丙会让球开始时在谁手中?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AD是BC边上的中线,点E是AD的中点;过点A作AF∥BC,交BE的延长线于F,连接CF. 
(1)求证:四边形ADCF是平行四边形;
(2)填空: ①当AB=AC时,四边形ADCF是形;
②当∠BAC=90°时,四边形ADCF是形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料: 2014年,是全面深化改革的起步之年,是实施“十二五”规划的攻坚之年,房山区经济发展稳中有升、社会局面和谐稳定,年初确定的主要任务目标圆满完成:全年地区生产总值和固定资产投资分别为530和505亿元;区域税收完成202.8亿;城乡居民人均可支配收入分别达到3.6万元和1.9万元.
2015年,我区较好实现了“十二五”时期经济社会发展目标,开启了房山转型发展的新航程:全年地区生产总值比上年增长7%左右;固定资产投资完成530亿元;区域税收完成247亿元;公共财政预算收入完成50.02亿元;城乡居民人均可支配收入分别增长8%和10%.
2016年,发展路径不断完善,房山区全年地区生产总值完成595亿元,固定资产投资完成535亿元,超额实现预期目标,区域税收比上一年增长4.94亿元,城乡居民可支配收入分别增长8.%和8.8%.
(摘自《房山区政府工作报告》)
根据以上材料解答下列问题:
(1)2015年,我区全年地区生产总值为亿元.
(2)选择统计图或统计表,将我区2014~2016年全年地区生产总值、固定资产投资和区域税收表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
①ac<0 ②2a+b=0 ③4a+2b+c>0 ④对任意实数x均有ax2+bx≥a+b
正确的结论序号为: . 
查看答案和解析>>
科目:初中数学 来源: 题型:
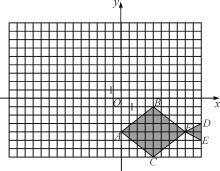
【题目】小金鱼在直角坐标系中的位置如图所示,根据图形解答下面的问题:
(1)分别写出小金鱼身上点A,B,C,D,E,F的坐标;
(2)小金鱼身上的点的纵坐标都乘以-1,横坐标不变,作出相应图形,它与原图案相比有哪些变化?
(3)小金鱼身上的点的横坐标都乘-1,所得图形与原图形相比有哪些变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“中秋”节前,朵朵的妈妈去超市购买了大小、形状、重量等都相同的五仁和豆沙月饼若干,放入不透明的盒中,此时从盒中随机取出五仁月饼的概率为 ![]() ;爸爸从盒中取出五仁月饼3只、豆沙粽子7只送给爷爷和奶奶后,这时随机取出五仁月饼的概率为
;爸爸从盒中取出五仁月饼3只、豆沙粽子7只送给爷爷和奶奶后,这时随机取出五仁月饼的概率为 ![]() .
.
(1)请你用所学知识计算:妈妈买的五仁月饼和豆沙月饼各有多少只?
(2)若朵朵一次从盒内剩余月饼中任取2只,问恰有五仁月饼、豆沙月饼各1只的概率是多少?(用列表法或树状图计算)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com