
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
①ac<0 ②2a+b=0 ③4a+2b+c>0 ④对任意实数x均有ax2+bx≥a+b
正确的结论序号为: . 
【答案】①②④
【解析】解:∵抛物线开口向上,
∴a>0,
∵抛物线与y轴的交点在x轴的下方,
∴c<0,
∴ac<0,故①正确.
∵对称轴x=﹣ ![]() =1,
=1,
∴2a=﹣b,
∴b+2a=0,故②正确;
根据图象知道
当x=2时,y=4a+2b+c<0,故③错误,
∵当x=1时,y最小=a+b+c,
∴ax2+bx+c≥a+b+c,
∴ax2+bx≥a+b,故④正确.
∴正确的结论序号为:①②④,
所以答案是:①②④.
【考点精析】认真审题,首先需要了解二次函数图象以及系数a、b、c的关系(二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)).


科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y= ![]() (k>0)的图象与BC边交于点E.
(k>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积为 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在Rt△ABC中,斜边AB=10,sinA= ![]() ,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,QN⊥CP于N.
,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,QN⊥CP于N.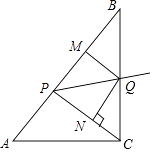
(1)当AP=CP时,求QP;
(2)若四边形PMQN为菱形,求CQ;
(3)探究:AP为何值时,四边形PMQN与△BPQ的面积相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M、N分别是正方形ABCD的边BC、CD上的点,已知:∠MAN=30°,AM=AN,△AMN的面积为1. 
(1)求∠BAM的度数;
(2)求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,∠B=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.
(1)如果点D在线段BC上运动,如图1:
①依题意补全图1;
②求证:∠BAD=∠EDC;
③通过观察、实验,小明得出结论:在点D运动的过程中,总有∠DCE=135°,.
小明与同学讨论后,形成了证明这个结论的几种想法:
想法一:在AB上取一点F,使得BF=BD,要证∠DCE=135°,只需证△ADF≌△DEC.
想法二:以点D为圆心,DC为半径画弧交AC于点F,要证∠DCE=135°,只需证△AFD≌△DCE.
想法三:过点E作BC所在直线的垂直线段EF,要证∠DCE=135°,只需证EF=CF.
…
请你参考上面的想法,证明∠DCE=135°
(2)如果点D在线段CB的延长线上运动,利用图2画图分析,∠DCE的度数还是确定的值吗?如果是,直接写出∠DCE的度数;如果不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D. 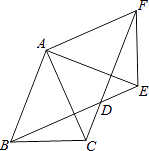
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象经过点(﹣1,0)、(5,0)、(0、﹣5).
(1)求此二次函数的解析式;
(2)当0≤x≤5时,求此函数的最小值与最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= ![]() 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( ) 
A.36
B.12
C.6
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com