
【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D. 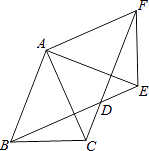
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
【答案】
(1)证明:∵△AEF是由△ABC绕点A按逆时针方向旋转得到的,
∴AE=AF=AB=AC=2,∠EAF=∠BAC=45°,
∴∠BAC+∠3=∠EAF+∠3,即∠BAE=∠CAF,
在△ABE和△ACF中
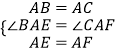 ,
,
∴△ABE≌△ACF,
∴BE=CF
(2)解:∵四边形ABDF为菱形,
∴DF=AF=2,DF∥AB,
∴∠1=∠BAC=45°,
∴△ACF为等腰直角三角形,
∴CF= ![]() AF=2
AF=2 ![]() ,
,
∴CD=CF﹣DF=2 ![]() ﹣2.
﹣2.
【解析】(1)根据旋转的性质得AE=AF=AB=AC=2,∠EAF=∠BAC=45°,然后根据“SAS”证明△ABE≌△ACF,于是根据全等三角形的性质即可得到结论;(2)根据菱形的性质得DF=AF=2,DF∥AB,再利用平行线的性质得∠1=∠BAC=45°,则可判断△ACF为等腰直角三角形,所以CF= ![]() AF=2
AF=2 ![]() ,然后计算CF﹣DF即可.
,然后计算CF﹣DF即可.
【考点精析】通过灵活运用菱形的性质和旋转的性质,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.


科目:初中数学 来源: 题型:
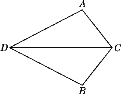
【题目】如图,点D为码头,A,B两个灯塔与码头的距离相等,DA,DB为海岸线,一轮船离开码头,计划沿∠ADB的平分线航行,在航行途中C点处,测得轮船与灯塔A和灯塔B的距离相等.试问:轮船航行是否偏离指定航线?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣![]() x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长和点C的坐标;
(2)求直线CD的解析式;
(3)y轴上是否存在一点P,使得S△PAB=![]() ,若存在,请求出点P的坐标;若不存在,请说明理由.
,若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(方程思想)如图,在铁路CD同侧有两个村庄A,B,它们到铁路的距离分别是15 km和10 km,作AC⊥CD,BD⊥CD,垂足分别为C,D,且CD=25 km.已知铁路旁有一个农副产品收购站E,且AE=BE,求CE的长.
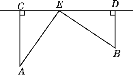
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
①ac<0 ②2a+b=0 ③4a+2b+c>0 ④对任意实数x均有ax2+bx≥a+b
正确的结论序号为: . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+2x+a﹣2=0.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)当该方程的一个根为1时,求a的值及方程的另一根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以x为自变量的二次函数y=﹣x2+(2m+2)x﹣(m2+4m﹣3)中,m为不小于0的整数,它的图象与x轴的交点A在原点左边,交点B在原点右边.
(1)求这个二次函数的解析式;
(2)设点C为此二次函数图象上的一点,且满足△ABC的面积等于10,请求出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com