
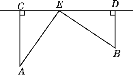
【题目】(方程思想)如图,在铁路CD同侧有两个村庄A,B,它们到铁路的距离分别是15 km和10 km,作AC⊥CD,BD⊥CD,垂足分别为C,D,且CD=25 km.已知铁路旁有一个农副产品收购站E,且AE=BE,求CE的长.
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为( )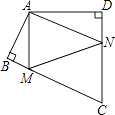
A.80°
B.90°
C.100°
D.130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题.

(1)将下面的表格补充完整:
正多边形的边数 | 3 | 4 | 5 | 6 | …… | 18 |
∠α的度数 |
|
|
|
| …… |
|
(2)根据规律,是否存在一个正n边形,使其中的∠α=20°?若存在,直接写出n的值;若不存在,请说明理由.
(3)根据规律,是否存在一个正n边形,使其中的∠α=21°?若存在,直接写出n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国国家邮政局公布的数据显示,2016年中国快递业务量突破313.5亿件,同比增长51.7%,快递业务量位居世界第一,业内人士表示,快递业务连续6年保持50%以上的高速增长,已成为中国经济的一匹“黑马”,未来中国快递业务仍将保持快速增长势头,以下是根据相关数据绘制的统计图,请你预估2017年全国快递的业务量大约为(精确的0.1)亿元. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M、N分别是正方形ABCD的边BC、CD上的点,已知:∠MAN=30°,AM=AN,△AMN的面积为1. 
(1)求∠BAM的度数;
(2)求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D. 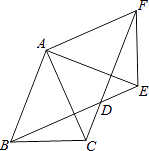
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师提出了一个问题:
我们知道,三角形的一个外角等于和它不相邻的两个内角的和,那么三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系?
(1)独立思考,请你完成老师提出的问题:
如图所示,已知∠DBC和∠BCE分别为△ABC的两个外角,试探究∠A和∠DBC,∠BCE之间的数量关系.

解:
⑵合作交流,“创新小组”受此问题的启发:分别作外角∠CBD和∠BCE的平分线BF和CF,交于点F(如图所示),那么∠A与∠F之间有何数量关系?请写出解答过程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com