
ЁОЬтФПЁПШчЙћвЛИіЖрБпаЮЕФИїБпЖМЯрЕШЃЌЧвИїФкНЧвВЖМЯрЕШЃЌФЧУДетИіЖрБпаЮОЭНазіе§ЖрБпаЮЃЌШчЭМЃЌОЭЪЧвЛзще§ЖрБпаЮЃЌЙлВьУПИіе§ЖрБпаЮжаЁЯІСЕФБфЛЏЧщПіЃЌНтД№ЯТСаЮЪЬтЃЎ

ЃЈ1ЃЉНЋЯТУцЕФБэИёВЙГфЭъећЃК
е§ЖрБпаЮЕФБпЪ§ | 3 | 4 | 5 | 6 | ЁЁ | 18 |
ЁЯІСЕФЖШЪ§ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ | ЁЁ ЁЁ |
ЃЈ2ЃЉИљОнЙцТЩЃЌЪЧЗёДцдквЛИіе§nБпаЮЃЌЪЙЦфжаЕФЁЯІС=20ЁуЃПШєДцдкЃЌжБНгаДГіnЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉИљОнЙцТЩЃЌЪЧЗёДцдквЛИіе§nБпаЮЃЌЪЙЦфжаЕФЁЯІС=21ЁуЃПШєДцдкЃЌжБНгаДГіnЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ60ЁуЃЌ45ЁуЃЌ36ЁуЃЌ30ЁуЃЌ10ЁуЃЛЃЈ2ЃЉЕБЖрБпаЮЪЧе§ОХБпаЮЃЌФмЪЙЦфжаЕФЁЯІС=20ЁуЃЛЃЈ3ЃЉВЛДцдкЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЖрБпаЮФкНЧКЭЙЋЪНЧѓГіЖрБпаЮЕФФкНЧКЭЃЌдйИљОнШ§НЧаЮФкНЧКЭЖЈРэЧѓГіМДПЩЃЛ
ЃЈ2ЃЉИљОнБэжаЕФНсЙћЕУГіЙцТЩЃЌИљОнЙцТЩЕУГіЗНГЬЃЌЧѓГіЗНГЬЕФНтМДПЩЃЛ
ЃЈ3ЃЉИљОнБэжаЕФНсЙћЕУГіЙцТЩЃЌИљОнЙцТЩЕУГіЗНГЬЃЌЧѓГіЗНГЬЕФНтМДПЩЃЎ
ЃЈ1ЃЉЬюБэШчЯТЃК
е§ЖрБпаЮЕФБпЪ§ | 3 | 4 | 5 | 6 | ЁЁ | 18 |
ЁЯІСЕФЖШЪ§ | 60Ёу | 45Ёу | 36Ёу | 30Ёу | ЁЁ | 10Ёу |
ЙЪД№АИЮЊЃК60ЁуЃЌ45ЁуЃЌ36ЁуЃЌ30ЁуЃЌ10ЁуЃЛ
ЃЈ2ЃЉДцдквЛИіе§nБпаЮЃЌЪЙЦфжаЕФЁЯІС=20ЁуЃЌ
РэгЩЪЧЃКИљОнЬтвтЕУЃК![]() =20ЁуЃЌ
=20ЁуЃЌ
НтЕУЃКn=9ЃЌ
МДЕБЖрБпаЮЪЧе§ОХБпаЮЃЌФмЪЙЦфжаЕФЁЯІС=20ЁуЃЛ
ЃЈ3ЃЉВЛДцдкЃЌРэгЩШчЯТЃК
МйЩшДцдке§ n БпаЮЪЙЕУЁЯІС=21ЁуЃЌЕУ ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌгж n ЪЧе§ећЪ§ЃЌ
ЃЌгж n ЪЧе§ећЪ§ЃЌ
ЫљвдВЛДцдке§ n БпаЮЪЙЕУЁЯІС=21ЁуЃЎ


 ПМЧАБиСЗЯЕСаД№АИ
ПМЧАБиСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЬтЁЃ 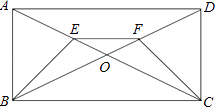
ЃЈ1ЃЉгУЪЪЕБЕФЗНЗЈНтЯТСавЛдЊЖўДЮЗНГЬЃКx2Љ6x+1=0ЃЎ
ЃЈ2ЃЉШчЭМЃЌвбжЊEЁЂFЗжБ№ЪЧОиаЮABCDЕФЖдНЧЯпACКЭBDЩЯЕФЕуЃЌЧвAE=DFЃЌЧѓжЄЃКBE=CFЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
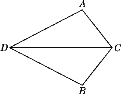
ЁОЬтФПЁПШчЭМЃЌЕуDЮЊТыЭЗЃЌAЃЌBСНИіЕЦЫўгыТыЭЗЕФОрРыЯрЕШЃЌDAЃЌDBЮЊКЃАЖЯпЃЌвЛТжДЌРыПЊТыЭЗЃЌМЦЛЎбиЁЯADBЕФЦНЗжЯпКНааЃЌдкКНааЭОжаCЕуДІЃЌВтЕУТжДЌгыЕЦЫўAКЭЕЦЫўBЕФОрРыЯрЕШЃЎЪдЮЪЃКТжДЌКНааЪЧЗёЦЋРыжИЖЈКНЯпЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§y1=ax+bЃЈaЁй0ЃЉЕФЭМЯѓгыyжсЯрНЛгкЕуAЃЌгыЗДБШР§КЏЪ§y2= ![]() ЃЈcЁй0ЃЉЕФЭМЯѓЯрНЛгкЕуBЃЈ3ЃЌ2ЃЉЁЂCЃЈЉ1ЃЌnЃЉЃЎ
ЃЈcЁй0ЃЉЕФЭМЯѓЯрНЛгкЕуBЃЈ3ЃЌ2ЃЉЁЂCЃЈЉ1ЃЌnЃЉЃЎ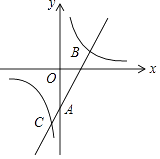
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЭМЯѓЃЌжБНгаДГіy1ЃОy2ЪБxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉдкyжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїPABЮЊжБНЧШ§НЧаЮЃПШчЙћДцдкЃЌЧыЧѓЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉЕФЖдГЦжсЮЊжБЯпx=Љ1ЃЌгыxжсЕФвЛИіНЛЕуAдкЕуЃЈЉ3ЃЌ0ЃЉКЭЃЈЉ2ЃЌ0ЃЉжЎМфЃЌЦфВПЗжЭМЯѓШчЭМЫљЪОЃЌдђЯТСа4ИіНсТлЃКЃКЂйb2Љ4acЃМ0ЃЛЂк2aЉb=0ЃЛЂлa+b+cЃМ0ЃЛЂмЕуMЃЈx1 ЃЌ y1ЃЉЁЂNЃЈx2 ЃЌ y2ЃЉдкХзЮяЯпЩЯЃЌШєx1ЃМx2 ЃЌ дђy1Ёмy2 ЃЌ Цфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ 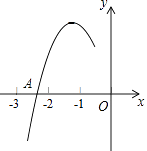
A.1Иі
B.2Иі
C.3Иі
D.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвдRtЁїABCЕФACБпЮЊжБОЖзїЁбOНЛаББпABгкЕуEЃЌСЌНгEOВЂбгГЄНЛBCЕФбгГЄЯпгкЕуDЃЌЕуPЮЊBCЕФжаЕуЃЌСЌНгEPЃЌADЃЎ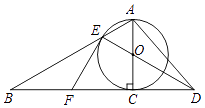
ЃЈ1ЃЉЧѓжЄЃКPEЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ3ЃЌЁЯB=30ЁуЃЌЧѓPЕуЕНжБЯпADЕФОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпy=Љ![]() x+4гыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂЕуBЃЌЕуDдкyжсЕФИКАыжсЩЯЃЌШєНЋЁїDABбижБЯпADелЕўЃЌЕуBЧЁКУТфдкxжсе§АыжсЩЯЕФЕуCДІЃЎ
x+4гыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂЕуBЃЌЕуDдкyжсЕФИКАыжсЩЯЃЌШєНЋЁїDABбижБЯпADелЕўЃЌЕуBЧЁКУТфдкxжсе§АыжсЩЯЕФЕуCДІЃЎ
ЃЈ1ЃЉЧѓABЕФГЄКЭЕуCЕФзјБъЃЛ
ЃЈ2ЃЉЧѓжБЯпCDЕФНтЮіЪНЃЛ
ЃЈ3ЃЉyжсЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЕУSЁїPAB=![]() ЃЌШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЌШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(ЗНГЬЫМЯы)ШчЭМЃЌдкЬњТЗCDЭЌВргаСНИіДхзЏAЃЌBЃЌЫќУЧЕНЬњТЗЕФОрРыЗжБ№ЪЧ15 kmКЭ10 kmЃЌзїACЁЭCDЃЌBDЁЭCDЃЌДЙзуЗжБ№ЮЊCЃЌDЃЌЧвCDЃН25 km.вбжЊЬњТЗХдгавЛИіХЉИБВњЦЗЪеЙКеОEЃЌЧвAEЃНBEЃЌЧѓCEЕФГЄЃЎ
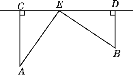
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁбOжаЃЌЯвABЫљЖдЕФСгЛЁЪЧдВжмГЄЕФ ![]() ЃЌЦфжадВЕФАыОЖЮЊ4cmЃЌЧѓЃК
ЃЌЦфжадВЕФАыОЖЮЊ4cmЃЌЧѓЃК 
ЃЈ1ЃЉЧѓABЕФГЄЃЎ
ЃЈ2ЃЉЧѓвѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com